| A
lower triangular matrix is a square
matrix in which all elements above the main diagonal are zeros. |
| Square
matrices for which aij
= aji
are called symmetric about the main
diagonal. |
| Examples
of the square matrices |
| |
The
diagonal matrix of order 4, |
|
The
identity matrix of order 3, |
|
| |
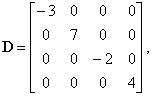 |
|
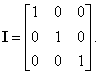 |
|
|
| |
The
upper triangular matrix of order 4, |
|
The
lower triangular matrix of order 4, |
|
| |
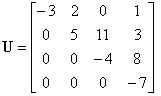 |
|
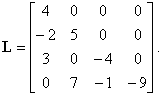 |
|
|
|
The
symmetric matrix of order 5, |
|
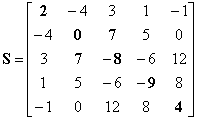 |
The
elements of the main diagonal are in bold. |
|
| A
matrix whose all elements are zero is called the null
matrix, written 0. |
|
| Vectors |
| A
matrix with only one row or one column is called a vector. |
| A
matrix with one row and n
columns is called a row vector. |
| A
matrix with one column and m
rows is called a column vector. |
|
| Transposition |
| The
transpose is the matrix derived from a given matrix by
interchanging the rows and columns. Thus, the |
|
transpose of a matrix A
of order
m
´
n
is another matrix
denoted AT
of order n
´
m. |
| Therefore,
to transpose means to interchange the rows and columns of a
matrix, that
is, |
| AT
= [aji],
where j
is the column and i
is the row of matrix A
= [aij]. |
| Example:
Given a matrix A
of order 3 ´
4, find the transpose AT.
|
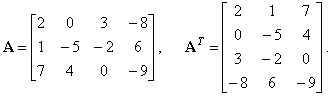 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
K |
|
 |
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|