|
|
Analytic Geometry (Coordinate Geometry) in Three-dimensional Space |
|
|
Point,
Line and Plane - orthogonal
projections, distances, perpendicularity of line and plane
|
Distance between parallel lines
example |
|
Distance between two
skew lines example |
|
|
|
|
|
|
|
|
Distance between parallel lines
|
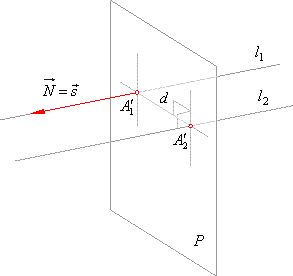
| Distance between two parallel lines we calculate as the distance between intersections of the lines and a plane
orthogonal to the given lines.
|
| The direction vector of the plane orthogonal to the given lines is collinear or coincides with their direction vectors
that is |
| N
= s = ai + b j + ck |
| By plugging any of two points, which are included in the equations of the given lines, into the equation of the plane,
determined is the parameter D, as well as determined is one
of the intersection points. |
|
 |
|
|
|
| Example:
Find the distance between given parallel lines, |
 |
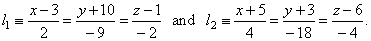| Solution: The direction vector of a plane orthogonal to
the parallel lines is collinear with the direction vectors
of these lines, so N =
s = 2i -
9 j - 2k.
|
|
Let the plane passes through the point
A´2(-5,
-3,
6) of the second line, then
|
|
A´2(-5,
-3,
6) =>
Ax +
By + Cz + D
= 0
or 2 · (-5)
-
9 · (-3)
+ (-2)
· 6 + D
= 0,
D
= -5
|
|
thus, the equation of the plane 2x
-
9y -
2z -
5 = 0, besides the point A´2(-5,
-3,
6) is the intersection of the second line and the plane.
|
|
The intersection of the first line and the plane
we calculate as follows,
|
|
|
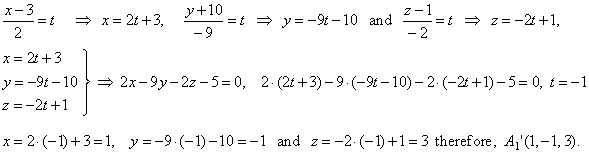
The distance between the intersection points
A´1
and A´2
is at the same time the distance between given lines, thus
|
|
|
|
|
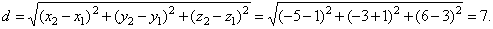
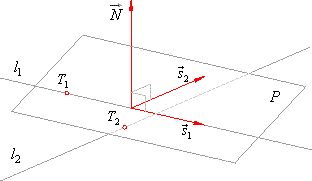
Distance between two skew lines
|
|
Through one of a given skew lines lay a plane parallel to another line and calculate the distance between any
point of that line and the plane.
|
| The direction vector of planes, which are parallel to both lines, is coincident with the vector product of direction vectors of given lines, so we can write |
| N
= s1 ´
s2 |
| A plane to
lie on the one of the given lines,
we should plug the point, that is included into the
equation of the line, into the equation of the plane
and so determined
is the parameter
D
of the plane.
|
|
 |
|
|
|
| Example:
Find the distance between given skew lines, |
 |
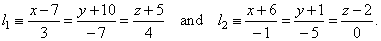| Solution: Through the line
l1
lay a plane parallel to the line
l2. The direction vector of the plane,
|
|
|
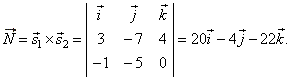
The point included in the equation of the line
l1
must satisfy the equation of the plane, so
|
|
P1(7, -10, -5)
=> Ax +
By + Cz + D
= 0,
20 · 7 + (-4)
· (-10)
+ (-22)
· (-5)
+ D
= 0,
|
|
D
= -290 thus, the equation of the plane
20x
-
4y -
22z -
290 = 0.
|
|
The distance between the point
T2(-6,
-1,
2), of the line
l2, and the plane which is parallel to it
|
|
|
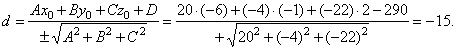
As was already mentioned, the sign of the square root is taken to be opposite to the sign of the parameter D.
|
|
Therefore, the negative value of the result only informs us that the point is positioned at the same side as
the origin of the coordinate system.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
J |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
