|
|
Analytic Geometry (Coordinate Geometry) in Three-dimensional Space |
|
|
Point,
Line and Plane - orthogonal
projections, distances, perpendicularity of line and plane
|
 Distance between
point and line example
Distance between
point and line example |
 Distance between point and plane
example
Distance between point and plane
example |
|
|
|
|
|
|
| Distance between point and line
|
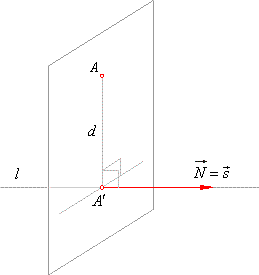
| The
distance d
between a point and a line we calculate as the distance between the given point
A(x1,
y1,
z1)
and its
orthogonal projection onto the given line using the formula for the distance
between two points. |
| The projection of the point onto the line is at the same time the
intersection point AŽ(xp,
yp,
zp) of the given line and a plane which
passes through the given point orthogonal to the given line, thus |
|
|
| where
d
is the distance between the given point and the given line. |
|
 |
|
|
| Example:
Find the distance between a point A(-3,
5, -2) and a line |
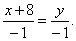 |
|
|
| Solution: Through the given point lay a plane perpendicular to the given line,
then as N =
s = -i -
j
and
|
| A(-3,
5, -2) =>
P
::
-x
-
y + D
= 0 gives
-1 · (-3)
-
1 · 5 + D
= 0, D
= 2 so,
P
::
-x
-
y + 2 = 0. |
| Then,
rewrite the given line into the parametric form to get its intersection
with the plane P, |
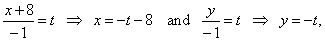 |
| plug
these variable coordinates of a point of the line into the plane to find
parameter t
that determine the intersection
point, |
| x
= -t
-
8 and y
= -t
=>
-x
-
y + 2
= 0 so
that -(-t
-
8) -(-t) +
2
= 0,
t
= -5 |
| therefore,
x
= -(-5)
-
8
= -3
and y
= -t
= -(-5)
= 5,
the intersection AŽ(-3,
5, 0). |
| The
distance between the point A
and the line equals the distance between points, A
and AŽ
thus, |
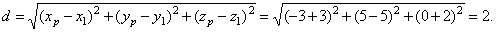 |
|
| Distance between point and plane
|
| We
use the formulas for the distance from a point to a plane
that are given in the two forms earlier in this chapter,
they are |
| - the Hessian normal form,
d = x0cosa
+ y0cosb
+ z0cosg
-
p |
| - and when a plane is given in general form, |
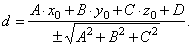 |
|
|
| The distance between a point and a plane can also be calculated using the formula for the distance between
two points, that is, the distance between the given point and its orthogonal projection onto the given plane.
|
|
|
| Example:
Given is a point A(4,
13, 11) and a plane x +
2y + 2z -
4 = 0, find the distance between the point
and the plane. |
| Solution: Through the given point draw a line orthogonal to the plane, so that
s = N =
i + 2 j + 2k
|
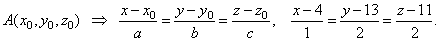
|
|
The intersection of the line and the plane,
|
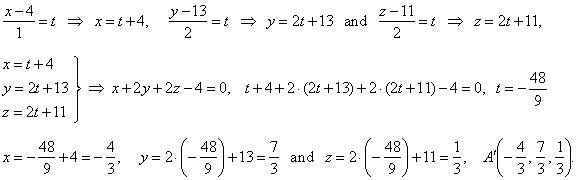
|
|
The distance between a point and the plane equals the distance between the point
A
and the intersection (or projection of the point
A onto the plane), thus
|
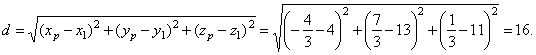
|
|
Check the result using the above formula,
|
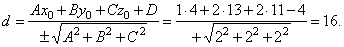
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
J |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |