|
|
Analytic Geometry (Coordinate Geometry) in Three-dimensional Space |
|
|
Point,
Line and Plane - orthogonal
projections, distances, perpendicularity of line and plane
|
 Plane laid through a given point, such that be parallel with two
skew lines, example
Plane laid through a given point, such that be parallel with two
skew lines, example |
 Plane laid through a given point, such that be parallel with two
parallel lines, example
Plane laid through a given point, such that be parallel with two
parallel lines, example |
|
|
|
|
|
|
|
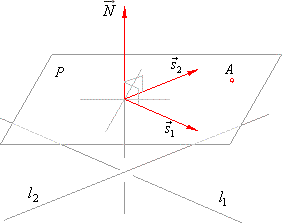
| Plane laid through a given
point such that be parallel with two skew lines |
| The normal vector of planes that are parallel with two skew lines is collinear to the vector product of direction |
| N
= s1 ´
s2 |
| The plane passes through a given point if
the coordinates of the point A(x0,
y0,
z0) satisfy the equation of the
plane that is |
| Ax0 +
By0 + Cz0 + D
= 0 |
| this condition determines the parameter
D
of the plane to be found. |
|
 |
|
|
| Example:
Given are skew lines, |
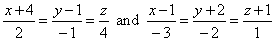 |
and the point
A(3, 2, 5),
|
|
| lay a
plane through the given point parallel with the given lines.
|
| Solution: From
the equations of the lines, s1
= 2i -
j +
4k
and s2
= -3i
-
2 j +
k,
so the normal vector of the plane
|
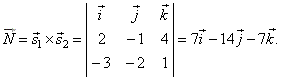 |
| Plug the point
A
into the equation of the plane to determine D, |
| A(3, 2, 5)
=>
7x -
14y
-
7z + D = 0
=>
7 · 3
-
14 · 2 -
7 · 5
+ D = 0,
D =
42
|
|
therefore, the equation of the plane 7x
-
14y
-
7z + 42 = 0. |
|
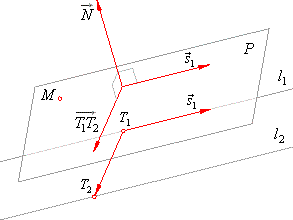
| Plane
laid through a given point such that be parallel with two parallel
lines |
| In this case, the normal vector of
the planes, which are parallel with two parallel lines, is collinear with the vector
product of the direction vector of one line and the vector
T1T2
that represents the difference of the |
|
radius vectors r2
-
r1,
of any of the points of the given lines, that is |
| N
= s1 ´
(r2
-
r1) |
| The
given point M(x0,
y0,
z0)
is a point of the plane, so it must satisfy the
condition, |
| Ax0 +
By0 + Cz0 + D
= 0. |
| And this is the way to determine the parameter
D
of the plane
to be found. |
|
 |
|
|
| Example:
Through the point O(0, 0, 0) lay a plane parallel to lines, |
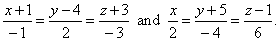 |
| Solution: Given lines are parallel since their direction vectors are collinear, i.e.,
|
| s1
= -i +
2 j -
3k and s2
= 2i
-
4 j + 6k
= -2 · (-i +
2 j -
3k)
= -2s1. |
| Offered points,
T1(-1,
4, -3)
and T2(0,
-5,
1), in the equations of lines, connected are by the vector, |
| T1T2
= r2
-
r1
= ( -5
j + k) -
(-i +
4 j -
3k)
= i -
9 j + 4k. |
| Therefore,
the normal vector of the plane |
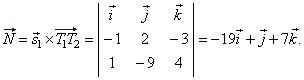 |
| The given point (the
origin
O), plugged into the equation of a plane,
|
| O(0, 0, 0)
=>
Ax +
By + Cz + D
= 0 gives
-19 · 0 + 1 · 0 + 7 · 0 + D
= 0,
D
= 0 |
| so the equation of the plane to be found is,
-19x +
y + 7z
= 0.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
J |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |