|
|
Analytic Geometry (Coordinate Geometry) in Three-dimensional Space |
|
|
Point,
Line and Plane - orthogonal
projections, distances, perpendicularity of line and plane
|
 Projection of a line onto a plane,
example
Projection of a line onto a plane,
example
|
|
|
|
|
|
|
|
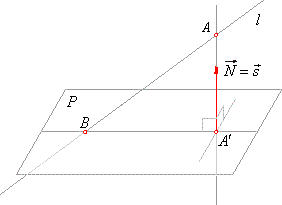
| Projection of a line onto a plane
|
| Orthogonal projection of a line onto a plane is a line or a point. If a given line is perpendicular to a plane, its
projection is a point, that is the intersection point with the plane, and its direction vector
s
is coincident with the normal vector N
of the plane. |
|
If a line is parallel with a plane then it is also parallel with its projection onto the plane and orthogonal to the normal vector of the plane that is |
| s
^ N
=> s
· N = 0. |
| Projection of a
line which is not parallel nor perpendicular to a plane, passes through their intersection
B and through the
projection A´
of any point
A
of the line onto the plane,
as shows the right figure. |
|
 |
|
|
| Example:
Determine projection of the line |
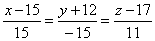 |
onto the plane |
|
| 13x -
9y + 16z -
69 = 0.
|
| Solution: First determine coordinates of the intersection point
of the line and the plane,
|
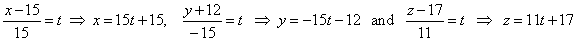 |
| plug
these variable coordinates of the line into the plane |
| x =
15t + 15, y
= -15t
-
12 and z
= 11t + 17 =>
13x -
9y + 16z -
69 = 0, |
| that
is, 13 · (15t + 15) - 9
· (-15t
-
12) + 16 · (11t + 17) -
69 = 0 => t = -1
thus, |
| thus,
x = 15t + 15 = 15 · (-1) +
15 = 0, y
= -15t
-
12
= -15
· (-1)
-
12
= 3 |
|
and z
= 11t + 17
= 11 · (-1) +
17
= 6 therefore, the
intersection B(0, 3,
6). |
| Then, find the projection
A´
of a point A(15, -12,
17) of the given line, onto the plane, as the intersection of the normal through the point
A, and the plane. |
| So,
write the equation of the normal |
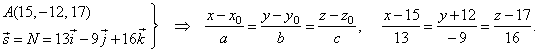 |
| Repeat
the same procedure to find the projection A′ as
for the intersection B,
that is |
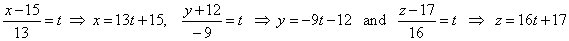 |
| plug these
variable coordinates of the normal into the equation of the given plane
to find the projection A´,
so |
| x =
13t + 15, y
= -9t
-
12 and z
= 16t + 17 =>
13x -
9y + 16z -
69 = 0, |
| 13(13t +
15) -
9(-9t
-
12) + 16(16t + 17) -
69 = 0, t
= -1. |
| Thus,
x = 13 · (-1) +
15 = 2, y
= -9
· (-1)
-
12
= -3
and z
= 16 · (-1) +
17
= 1, A´(2,
-3, 1). |
| Finally,
as the projection of the given line onto the given plane passes through
the intersection B
and the projection A´ then,
by plugging their coordinates into the equation of the line through two
points |
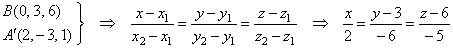 |
| obtained
is the equation of the projection. |
|
| Example:
Projection of the line |
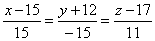 |
onto the plane
13x -
9y + 16z -
69 = 0,
|
|
| the
same
as in the above example, can be calculated applying simpler method.
|
| Solution: Intersection of the given plane and
the orthogonal plane through the given line, that is, the plane
through three points, intersection point B, the point
A
of the given line and its projection A´
onto the plane, is
at the same time projection of the given line onto the given
plane, as shows the right figure.
|
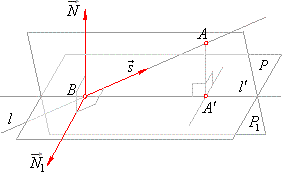
| The direction vector
N1, of the plane determined by three
points A,
B and
A´, is the result of the vector product of the
normal vector of the given plane and the direction vector
s of
the given line, that is |
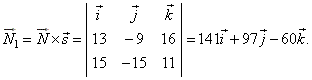 |
|
 |
|
| By
plugging the point A(15,
-12,
17) into the equation of the plane, |
| A(15,
-12,
17)
=> 141x
+
97y -
60z + D = 0
=>
141 · 15
+
97 · (-12)
-
60 · 17 + D =
0,
D = 69
|
| obtained
is the equation of the plane P1
::
141x + 97y -
60z + 69
= 0. |
| Finally, the line of the intersection
l´
of the given plane |
| P
::
13x -
9y + 16z -
69 = 0 and the plane P1
::
141x + 97y -
60z + 69 = 0 |
| is at the same time the projection of
the given line onto the given plane. |
| To
check the obtained result, write the vector product of normal vectors of planes
P
and
P1,
|
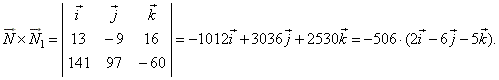 |
| therefore,
N
´
N1
= ls
the vector product is collinear with the direction vector of the intersection line,
what proves
the result. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
J |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |