|
|
Analytic Geometry (Coordinate Geometry) in Three-dimensional Space |
|
|
Point,
Line and Plane - orthogonal
projections, distances, perpendicularity of line and plane
|
Through a given point lay a line perpendicular to a given
line
example
|
|
Projection
of a line onto a plane, example
|
|
|
|
|
|
|
| Through a given point lay a line perpendicular to a given line
|
| A line which will pass through a given point perpendicular to a given line will lie in a plane that is
perpendicular to the given line and which passes through the given point. |
| The equation of that line is then
determined by two points, the given point and by its projection onto the given line or the intersection with the
plane. |
|
| Example: Through the point
A(-6,
-3, 4)
pass a line perpendicular to the line |
 |
|
| Solution:
Through the given point lay a plane perpendicular to the given line,
therefore |
| N =
s = 3i -
4j -
3k. |
|
Plug the point A
into the plane,
|
| A(-6,
-3, 4)
=>
3x
-
4y -
3z + D = 0,
D
=
18. |
| So, the equation of the plane |
| P
::
3x -
4y -
3z + 18 = 0. |
| The intersection
AŽ, as the common point of the given line
and the plane P, can be determined by plugging its parametrically expressed coordinates
into the equation of the plane, that is |
|
 |
|
 |
| plug
these variable coordinates of a point that moves along the line AAŽ
into the plane P |
| 3 · (3t + 2) - 4 · (-4t -
1) -
3 · (-3t -
2) + 18 = 0,
t = -1. |
| Thus,
determined is parameter t
such that the point AŽ
lies onto the lines l
and l1
and the plane P,
so that |
| x =
3t + 2 = 3 · (-1)
+ 2 = -1, y =
-4t -
1 = -4
· (-1)
-
1 = 3 and z =
-3t
-
2 = -3(-1)
-
2 = 1 |
| the
coordinates of the intersection AŽ(-1,
3, 1). |
| To
write the equation of the line l1
through the points, A(-6,
-3, 4)
and AŽ(-1,
3, 1), that is perpendicular to the
given line l,
we should calculate its direction vector and include one of its points. |
| The
direction vector s1
we get as the difference between positions vectors of the points, A
and AŽ, |
| s1
= rA -
rA′ = (-6i
-
3 j
+ 4k) -
(-i
+ 3 j
+ k) = -5i
-
6j
+ 3k |
| then,
we plug any of its points, A
or AŽ
to form the equation of the line l1.
So, let plug the point A |
 |
| Let
check the result by calculating the scalar product of the vectors,
s
and s1
|
| s · s1 =
(3i -
4j -
3k) · (-5i
-
6j + 3k) = 3 · (-5)
+ (-4) · (-6)
+ (-3) · 3
= 0, since s
^ s1. |
|
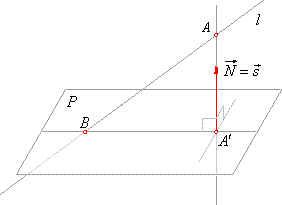
| Projection of a line onto a plane
|
| Orthogonal projection of a line onto a plane is a line or a point. If a given line is perpendicular to a plane, its
projection is a point, that is the intersection point with the plane, and its direction vector
s
is coincident with the normal vector N
of the plane. |
|
If a line is parallel with a plane then it is also parallel with its projection onto the plane and orthogonal to the normal vector of the plane that is |
| s
^ N
=> s
· N = 0. |
| Projection of a
line which is not parallel nor perpendicular to a plane, passes through their intersection
B and through the
projection AŽ
of any point
A
of the line onto the plane,
as shows the right figure. |
|
 |
|
|
| Example:
Determine projection of the line |
 |
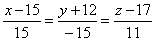onto the plane |
|
| 13x -
9y + 16z -
69 = 0.
|
| Solution: First determine coordinates of the intersection point
of the line and the plane,
|
 |
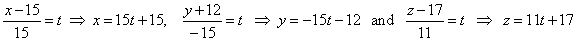| plug
these variable coordinates of the line into the plane |
| x =
15t + 15, y
= -15t
-
12 and z
= 11t + 17 =>
13x -
9y + 16z -
69 = 0, |
| that
is, 13 · (15t + 15) - 9
· (-15t
-
12) + 16 · (11t + 17) -
69 = 0 => t = -1
thus, |
| thus,
x = 15t + 15 = 15 · (-1) +
15 = 0, y
= -15t
-
12
= -15
· (-1)
-
12
= 3 |
|
and z
= 11t + 17
= 11 · (-1) +
17
= 6 therefore, the
intersection B(0, 3,
6). |
| Then, find the projection
AŽ
of a point A(15, -12,
17) of the given line, onto the plane, as the intersection of the normal through the point
A, and the plane. |
| So,
write the equation of the normal |
 |
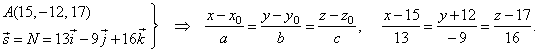| Repeat
the same procedure to find the projection A′ as
for the intersection B,
that is |
 |
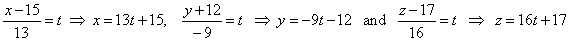| plug these
variable coordinates of the normal into the equation of the given plane
to find the projection AŽ,
so |
| x =
13t + 15, y
= -9t
-
12 and z
= 16t + 17 =>
13x -
9y + 16z -
69 = 0, |
| 13(13t +
15) -
9(-9t
-
12) + 16(16t + 17) -
69 = 0, t
= -1. |
| Thus,
x = 13 · (-1) +
15 = 2, y
= -9
· (-1)
-
12
= -3
and z
= 16 · (-1) +
17
= 1, AŽ(2,
-3, 1). |
| Finally,
as the projection of the given line onto the given plane passes through
the intersection B
and the projection AŽ then,
by plugging their coordinates into the equation of the line through two
points |
 |
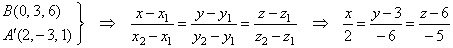| obtained
is the equation of the projection. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
J |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
