Comparison of general form and the Hessian normal form of equations of a plane, The distance of a point to a plane, Angle between two planes

Coordinate Geometry (Analytic Geometry) in Three-dimensional Space

Plane in a three-dimensional (3D) coordinate system

Comparison of the general form and the Hessian normal form of equations of a plane

The distance of a point to a plane - plane given in general form

Angle (dihedral angle) between two planes

Comparison of general form and the Hessian normal form of equations of a plane

Coefficients, A, B and C, beside coordinates x, y and z, of the general form of equation

Ax + By + Cz + D = 0

are the components of the normal vector N = Ai + Bj + Ck, while in the Hessian’s equation

x · cosa + y · cosb + z · cosg - p = 0,

on that place, there are components (the direction cosines) of the unit vector N° of the same vector.

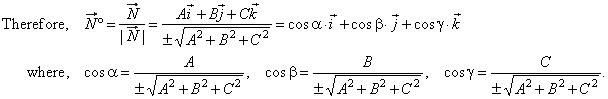Thus, to convert from general form to the Hessian normal form, divide the general form of equation by

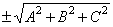taking the sign of the square root opposite to the sign of D, where D is not 0

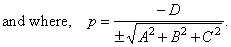The distance of a point to a plane - plane given in general form

Let replace in the Hessian formula for the distance d = x₀ · cosa + y₀ · cosb + z₀ · cosg - p, the direction cosines and the length of the normal p, by coefficients of the general form, to obtain

the formula for the distance of a point to a plane given in the general form.

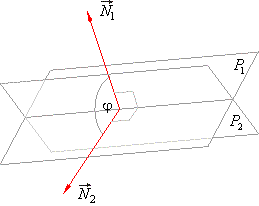
Angle (dihedral angle) between two planes

The angle subtended by normals drawn from the origin to the first and second plane, that is, the angle which form the normal vectors of the given planes is

the angle between two planes.

If planes are parallel normal vectors are collinear that is,

N₁ = lN₂ <=> j = 0°,

and if planes are orthogonal, then their normal vectors are orthogonal too, so their scalar product is zero,

N₁ · N₂ = 0 <=> j = 90°.

Example: Find the angle between planes, P₁ :: 2x - y + 4z - 3 = 0 and P₂:: -x - 3y + 5z + 6 = 0.

Solution: Thus,

N₁ = 2i - j + 4k and N₂ = -i - 3j + 5k, then

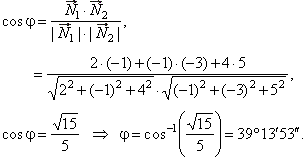Pre-calculus contents J