|
|
Analytic Geometry (Coordinate Geometry) in Three-dimensional Space |
|
|
Line
and Plane
|
The line of intersection of two planes
|
|
Projection of a line onto coordinate planes
|
|
How determine two planes of which, a given line is their
intersection line
|
|
|
|
|
|
|
| Line
and Plane
|
| The line of intersection of two planes
|
| Two planes are either parallel or they intersect in a line. If planes are parallel, their coefficients of coordinates
x,
y
and z
are proportional, that is
|
 |
|
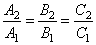and then, the vector product of their normal vectors is zero
|
| N1
´
N2
= 0. |
|
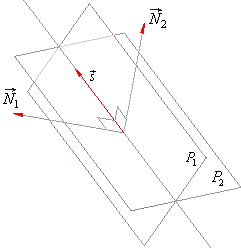
When two planes intersect, the vector product of their normal
vectors equals the direction vector s
of their line of intersection, |
| N1
´
N2
= s. |
|
To be able to write the equation of a line of intersection of two
planes we still need any point of that line. |
|
 |
|
| We
can use the intersection point of the line of intersection of two planes
with any of coordinate planes (xy,
xz or
yz plane)
as that point. |
|
| Example:
Given are planes, P1
:: -3x
+ 2y -
3z -
1 = 0 and P2
:: 2x -
y -
4z + 2 = 0, find the line of
intersection of the two planes.
|
| Solution: Since
the equation of the plane and its normal, |
| P
º
Ax + By
+ Cz + D = 0
and N =
Ai + Bj + Ck
then, N1
= -3i
+ 2j -
3k and N2
= 2i -
j -
4k, |
 |
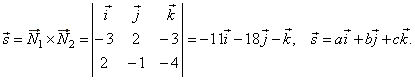| To write the equation of the line of intersection, i.e., |
 |
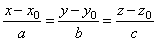| we still need the coordinates
of any of its point P(x0,
y0, z0). |
| Let this point be the intersection of the intersection line and the
xy
coordinate plane. |
|
Then, coordinates of the
point of intersection (x,
y, 0) must satisfy equations of the given planes. |
| Therefore,
by plugging z = 0
into P1
and P2
we get, |
 |
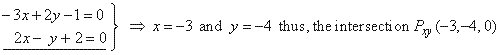| so,
the line of intersection is |
 |
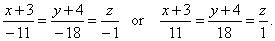| Using the same method we can check validity of obtained equation by calculating coordinates of another intersection point of the intersection line and the
yz
coordinate plane, and plug them into mentioned equation. |
| So,
coordinates of the intersection (0,
y, z) must satisfy equations of both
given planes |
 |
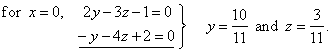| Now,
plug the coordinates of the intersection point Pyz
into the equation of the line of intersection |
 |
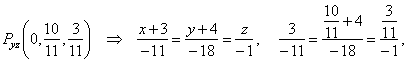| so, obtained equation is valid. |
|
| Projection of a line onto coordinate planes
|
| In the equation of a line, |
 |
| represents the orthogonal projection
of the given line onto the xy
coordinate plane. |
| At the same time, it is
spatial equation of the plane, which passes through the given line, and
is perpendicular to
the xy coordinate plane.
Similarly, |
 |
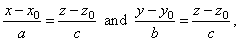| represent
the equations of the projections of the given line onto the xz and the
yz coordinate
plane respectively. |
| While, in relation to space, they are
the equations of planes passing through the given line orthogonal to the
xz and the
yz
coordinate planes respectively. |
|
| Example:
Find the (orthogonal) projections of the line |
 |
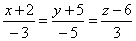onto coordinate planes and |
|
| find the coordinates of the intersection points of the line with the coordinate planes. |
| Solution: Equation |
 |
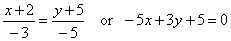is projection of the given line onto the
xy |
|
| coordinate plane,
i.e., it is the equation of the plane passing through the given line orthogonal to the
xy
plane, or it is the trace of that
plane in the xy
plane. |
| While the equations, |
 |
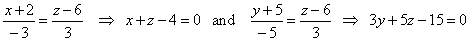| are the
projections of the given line onto the xz
plane and yz
plane respectively, i.e., they are the equations of planes
which are orthogonal onto these coordinate planes passing through the given line. |
| The coordinates of the intersection
point of the given line and the xy
coordinate plane we calculate by plugging z = 0 into the
equation of the given line that is, |
 |
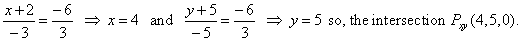| Similarly, the intersection
point of the given line and the xz
coordinate plane we calculate by plugging y
= 0, |
 |
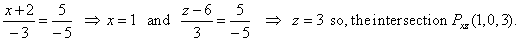| The intersection of the given line and the
yz
coordinate plane we calculate by plugging x
= 0 into the equation
of the given line that is |
 |
|
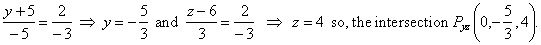| How determine two planes of which a given line is their
intersection line
|
| Through a given line |
|
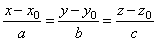lay two planes each of which is orthogonal to one of the |
|
| coordinate planes. |
| That way, given line will be determined by any of
the following pairs of
equations, |
 |
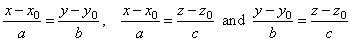| as the intersection line of the corresponding planes
(each of which is perpendicular to one of the three coordinate
planes). |
|
| Example:
Given is a line |
 |
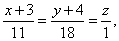find two planes of which given line is the intersection line. |
|
Solution: By eliminating the part of equation which contains
x-coordinates determined is a plane which
passes through the given line orthogonal to the yz
coordinate plane that is |
 |
| Therefore,
P1 ::
y -
18z + 4 = 0
with N1
= j -
18k and
P2
:: x -
11z + 3 = 0 with N2
= i -
11k. |
| The obtained result is correct if the vector product of the corresponding normal vectors,
N1
and N2
of the planes
equals the direction vector s
of the given line, so |
 |
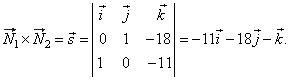| By calculating the coordinates of the intersection point, of the line of intersection represented by obtained
two planes, and the coordinate planes, by plugging successively, z = 0,
y = 0 and
x = 0 into their equations, we can prove that the result coincides with that in the
first example of this section, because it is the same line. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
J |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
