|
|
Analytic Geometry (Coordinate Geometry) in Three-dimensional Space |
|
|
Line
and Plane
|
How determine two planes of which, a given line is their
intersection line
|
|
Intersection point of a line and a plane
|
|
Points, Lines and planes relations in 3D space, examples
|
|
|
|
|
|
|
| How determine two planes of which a given line is their
intersection line
|
| Through a given line |
 |
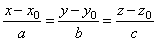lay two planes each of which is orthogonal to one of the |
|
| coordinate planes. |
| That way, given line will be determined by any of
the following pairs of
equations, |
 |
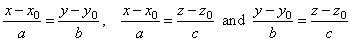| as the intersection line of the corresponding planes
(each of which is perpendicular to one of the three coordinate
planes). |
|
| Example:
Given is a line |
 |
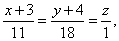find two planes of which given line is the intersection line. |
|
Solution: By eliminating the part of equation which contains
x-coordinates determined is a plane which
passes through the given line orthogonal to the yz
coordinate plane that is |
 |
| Therefore,
P1 ::
y -
18z + 4 = 0
with N1
= j -
18k and
P2
:: x -
11z + 3 = 0 with N2
= i -
11k. |
| The obtained result is correct if the vector product of the corresponding normal vectors,
N1
and N2
of the planes
equals the direction vector s
of the given line, so |
 |
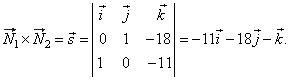| By calculating the coordinates of the intersection point, of the line of intersection represented by obtained
two planes, and the coordinate planes, by plugging successively, z = 0,
y = 0 and
x = 0 into their equations, we can prove that the result coincides with that in the
first example of this section, because it is the same line. |
|
| Intersection point of a line and a plane
|
| The point of intersection is a common point of a line and a plane. Therefore, coordinates of intersection must
satisfy both equations, of the line and the plane. |
| The parametric equation of a line, |
| x =
x0 + at,
y = y0
+ bt and
z
= z0 + ct |
| represents coordinates of any point of
the line expressed as the function of a variable parameter t
which makes
possible to determine any point of the line according to given condition. |
| Therefore, by plugging these variable coordinates of a point of the line into
the given plane determine what value
must have the parameter t,
this point to be the common point of the line and the plane. |
|
| Example:
Given is a line |
 |
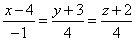and a plane
4x -
13y + 23z -
45 = 0, find the
|
|
| intersection
point of the line and the plane. |
| Solution: Transition from the symmetric to the parametric form
of the line
|
 |
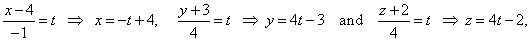| by plugging these variable coordinates
into the given plane we will find the value of the parameter t
such that these
coordinates represent common point of the line and the plane, thus |
| x =
-t +
4, y
= 4t -
3 and z
= 4t -
2 => 4x -
13y + 23z -
45 = 0 |
| which
gives, 4 · (-t +
4) - 13 · (4t -
3) + 23 · (4t -
2) -
45 = 0 Þ
t = 1. |
| Thus,
for t = 1
the point belongs to the line and the plane, so |
| x =
-t +
4 = -
1+ 4 = 3, y =
4t -
3 = 4 · 1 -
3 = 1 and z =
4t -
2 = 4 · 1 -
2 = 2. |
| Therefore, the intersection point
A(3,
1,
2) is the point which is at the same time on the line and the plane. |
|
| Points, Lines and planes relations
in 3D space, examples
|
| Example:
Through the line |
 |
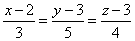lay
a plane to be parallel to the
y-axis, determine
|
|
| the
equation of the plane. |
| Solution: Write the line as the intersection of two planes to be able to form the sheaf of planes, therefore
|
 |
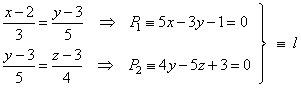| P1 and
P2
are the planes of which the given line is intersection and which are perpendicular to the coordinate
planes,
xy
and yz
respectively.
|
| Form the equation of a sheaf to determine the parameter
l according to
the given condition |
| P1
+ lP2 = 0
or (5x
-
3y -
1)
+ l(4y
-
5z + 3) = 0 |
| then,
5x
+ (-
3
+ 4l) ·
y -
5lz +
(3l
-
1) = 0
and Ns
= 5i + (-
3
+ 4l)
j -
5lk |
|
is the equation of planes that all intersect at the given line
and the normal vectors of which are perpendicular to the direction vector
s
of the line.
|
|
As the plane to be found should be parallel with the
y-axis, then the normal vector
of the sheaf Ns
must be perpendicular to the unit vector
j of the
y-axis that is, the scalar product of the normal vector of the plane
and the unit vector
j
must be zero, thus
|
|
Ns
^
j
=>
Ns
·
j = 0.
|
|
Since a scalar product of two vectors expressed by their coordinates is
|
|
a · b = axbx +
ayby + azbz
and since j
= 0 · i + 1 ·
j + 0 · k
|
|
then,
Ns
·
j = 5 · 0 + (-
3
+ 4l) · 1 + (-5l)
· 0 = 0
=>
l
= 3/4.
|
|
By plugging l
= 3/4 into (5x
-
3y -
1)
+ l(4y
-
5z + 3) = 0 obtained
is 4x
-
3z + 1 = 0
|
|
the plane through the given line that
is parallel to the
y-axis.
|
|
|
| Example:
Through the line |
|
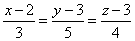(the
same as in the previous example) lay a plane
|
|
| orthogonal to the
plane
4x
-
2y + z -
4 = 0 and determine its equation.
|
| Solution: Write given line as the intersection of two planes (like in
the above example) to form the equation
|
|
of a
sheaf,
5x
+ (-
3
+ 4l) ·
y -
5lz +
(3l
-
1) = 0
and Ns
= 5i + (-
3
+ 4l)
j -
5lk
|
|
that is the plane parameter l
of which should be determined so the plane to be perpendicular to the given plane.
|
|
In this case, the normal vector of the sheaf
Ns
and the normal vector of the given plane N
= 4i -
2 j + k, are
orthogonal to each other, therefore
|
|
Ns
^ N
=>
Ns
· N = 0 that
is, 5 · 4 + (-
3
+ 4l) · (-2)
+ (-5l) · 1 = 0
=> l =
2.
|
|
Then, by plugging l
= 2 into 5x
+ (-
3
+ 4l) ·
y -
5lz +
(3l
-
1) = 0
|
|
obtained is 5x
+ 5y -
10z + 5 = 0
or x
+ y -
2z + 1 = 0
|
|
the equation of the plane which passes through the given line perpendicular to the given plane.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
J |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
