|
| Coordinate
Geometry (Analytic Geometry) in Three-dimensional Space |
|
|
Plane
in a three-dimensional (3D) coordinate system |
Equations of
a plane in a coordinate space
|
|
The intercept
form of the equation of a plane |
|
A plane in a 3D
coordinate system, examples |
|
Equation of the
plane through three points, example |
|
The distance between a point and a
plane - plane given in Hessian normal form
|
|
|
|
|
|
|
| Equations of a plane in a coordinate space
|
|
| The intercept form of the equation of a
plane
|
| If,
l,
m
and n
are the intercepts of
x,
y
and z
axes and a plane respectively, then projections of these segments in
direction of the normal drawn from the origin to the
plane are all equal to the length of the normal, that is
|
 |
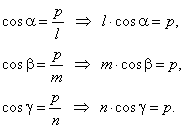| By plugging these values of cosines into Hessian
|
| normal
form of the equation of plane, obtained is |
|
|
| the intercept form of the equation of plane. |
|
 |
|
|
| A
plane in
a
3D coordinate system,
examples |
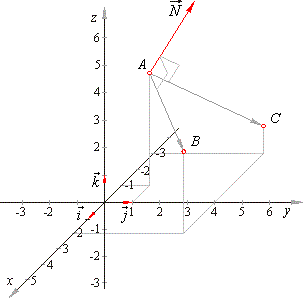
| Example:
Find the equation of
the plane through three points, A(-1,
1, 4), B(2,
4, 3)
and C(-3,
4, 1).
|
| Solution: |
| Equation of a plane
Ax
+ By
+ Cz
+ D = 0 is determined by
the components (the
direction cosines)
of the normal vector N
= Ai + Bj
+ Ck and
the coordinates of any point of the plane. |
| The normal vector is perpendicular to the plane determined by given
points, and as the vector |
| AB
= rB -
rA
= (2i + 4j + 3k)
-
(-i
+ j + 4k)
|
|
rB
-
rA
= 3i + 3j -
k,
and the vector
|
|
AC =
rC -
rA
= -2i
+ 3j -
3k
|
| then,
|
|
 |
|
 |
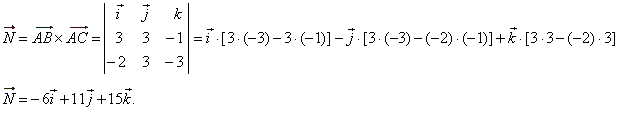| By plugging the coordinates, of any given point, into equation
of the plane determines the value of the coefficient
D.
Thus, plugging |
| A(-1,
1, 4) into
-
6x
+ 11y + 15z + D = 0
gives -
6
· (-1)
+ 11
· 1
+ 15
· 1
+ D = 0, D = -77. |
| Therefore,
-
6x + 11y + 15z -
77 = 0 is the equation of the plane
the given points lie on. |
| The coordinate of the remaining two points
B
and C
must also satisfy the obtained equation, prove. |
|
| Example:
Given are points,
A(-1,
1, 1)
and B(3,
-2,
6), find the equation of a plane which is normal to
the
vector
AB
and passes through the point A.
|
| Solution:
According to the given conditions
the vector
AB
= N
so,
|
| N
= rB -
rA
= (3i -
2j + 6k)
-
(-i
+ j + k) = 4i
-
3j + 5k
|
| As the plane should pass through the point
A |
| plug
A(-1,
1, 1) into
4x -
3y + 5z + D = 0
=>
4 · (-1)
-
3 · 1
+ 5
· 1
+ D = 0,
D = 2 |
| Therefore,
the equation of the plane P
::
4x -
3y + 5z + 2 = 0. |
|
|
| Example:
Segments that a plane cuts on the axes,
x
and y, are
l = -1 and
m = -2
respectively, find the standard or general equation of the plane if it passes through the point
A(3, 4, 6).
|
| Solution:
As the given point A(3, 4,
6) and the segments, l =
-1 and
m = -2
must satisfy the intercept
|
| form of the equation of plane,
then |
 |
|
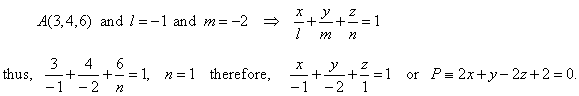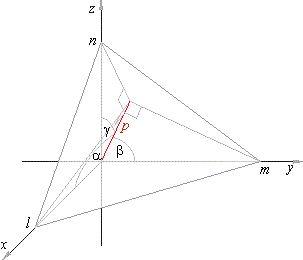
| The distance between a point and a
plane - plane given in Hessian normal form
|
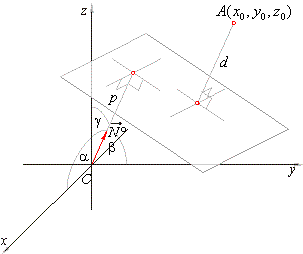
| Distance from a point
A0(x0,
y0, z0)
to a plane is taken to be positive if the given point is on the one side while the origin is on the other side regarding to the
plane, as is in
the right figure. |
| Through the point
A
lay a plane parallel to the given plane. |
| The length of a normal segment from the origin to the plane through
A,
written in the normal form, is p +
d. |
| As the point A
lies in that plane its coordinates must satisfy the equation |
| x0
· cosa
+ y0 · cosb
+ z0 · cosg
= p +
d. |
|
Thus, the
distance of the point to the given
plane is
|
|
d
= x0
· cosa
+ y0 · cosb
+ z0 · cosg -
p
|
|
|
|
 |
|
| To express the distance
d
in terms of the coefficients of the equation of a plane given in the general or
standard form, we should examine the relations of
the two forms of equations. |
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
J |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
