|
| Coordinate
Geometry (Analytic Geometry) in Three-dimensional Space |
|
|
|
|
Points, lines and planes in three-dimensional coordinate
system represented by vectors |
Equations of a line in space |
|
The
vector equation of a line
|
|
The parametric equations of a line
|
|
Equation of a line defined by
direction vector and a point - Symmetric equation of a line |
|
Line given by two points
|
|
Distance between two given points
|
|
Orthogonal projection of a line in
space onto the xy
coordinate plane |
|
|
|
|
|
|
| Equations of a line in space |
| The
vector equation of a line
|
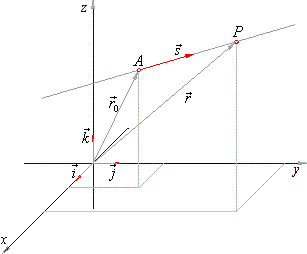
| Through a given point
A(x0,
y0, z0), which is determined by position vector
r0
= x0i + y0 j
+ z0k, passes a
line directed by its direction vector s
= ai + bj
+ ck. |
| Thus, the position of any point
P(x,
y, z) of a line is
then uniquely determined by a
vector |
|
|
| which is called the vector equation of a
line. |
| That is,
a radius vector r
= xi + y j
+ zk of every
point of the line, represents the sum of the radius vector r0,of the
given point, and a vector t
· s collinear to the vector
s, where t
is a parameter which can take any real value
from -
oo
to +
oo
. |
|
 |
|
|
| The parametric equations of a line
|
| By writing the above vector equation of a line in
the component form
|
 |
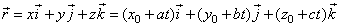| obtained are components of the vector
r, |
x
= x0 + at,
y = y0 +
bt and z
= z0 + ct |
which, at the same
|
|
| time, represent coordinates of any point of the line expressed as the function of a variable
parameter
t.
|
| That is why they are called the
parametric equation of a line.
|
|
| Equation of a line defined by
direction vector and a point - Symmetric equation of a line |
| Now,
let express t
from the above parametric equations
|
 |
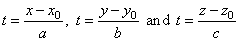| so, by equating
obtained is
|
|
|
| equation of a line passing through a point
A(x0,
y0, z0)
and given direction vector
s
= ai + bj
+ ck. |
| Scalar components (or the coordinates),
a,
b, and
c, of the direction vector
s, are |
|
|
| or the direction cosines
|
|
|
| that
is, the cosines of the angles that a line forms by the coordinates axes
x,
y
and
z, or the scalar components of
the unit vector of the direction vector
s
|
|
|
|
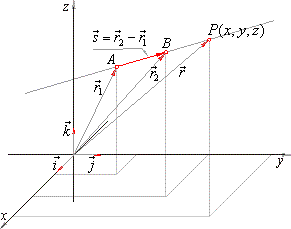
| Line given by two points
|
| A line through points
A
and B, determined by their position vectors, |
| r1
= x1i + y1 j
+ z1k
and r2
= x2i + y2 j
+ z2k, |
| has the direction vector
s
= r2 -
r1 so that its vector equation is |
|
|
| If we write this equation in the component form that is |
 |
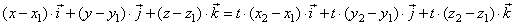| by equating corresponding scalar components |
 |
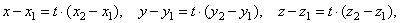| and by
eliminating parameter t |
|
|
| obtained is
equation of a line through two given |
| points, A(x1,
y1, z1)
and B(x2,
y2, z2). |
| The direction cosines are, |
 |
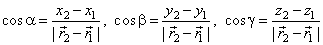| where |
 |
|
 |
|
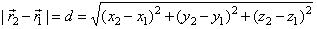| is the
distance between given points
A
and
B. |
| If, for example, in the above equation of a line through two points in a space, we take that
z
coordinate of both given points
is zero, we obtain known equation of a line through two points in a coordinate plane, i.e.,
|
 |
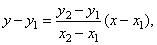| and at the same time,
it is the equation of the orthogonal projection of a line
in 3D space onto the xy coordinate
plane.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
J |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
