|
|
|
|
|
|
| The
graphs
of algebraic
and transcendental functions |
| Elementary
functions are, Algebraic functions
and Transcendental functions |
| Algebraic
functions |
|
· The
polynomial function
f (x) =
y = anxn
+ an-1xn-1
+ an-2xn-2
+
.
. . +
a2x2
+
a1x + a0 |
|
y
=
a1x
+ a0
- Linear
function |
|
y
=
a2x2
+
a1x + a0
-
Quadratic
function |
|
y
=
a3x3
+
a2x2
+
a1x + a0
-
Cubic
function |
|
y
=
a4x4
+
a3x3
+
a2x2
+
a1x + a0
-
Quartic
function |
|
y
=
a5x5
+ a4x4
+
a3x3
+
a2x2
+
a1x + a0
-
Quintic
function |
|
- - - -
- - - - - - - - -
- - - - - - - -
- - - - - - - - |
|
| The
graphs of rational functions |
| ·
Rational
functions - a ratio of two polynomials |
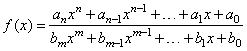 |
|
-
Reciprocal
function |
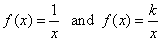 |
| |
-
Translation of the reciprocal function,
called linear rational function. |
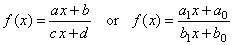 |
|
|
| Basic
properties of rational functions |
| The
functions that most likely have vertical, horizontal and/or
slant asymptotes are rational functions. |
| So,
vertical asymptotes occur when the
denominator of the simplified rational function is equal to 0.
Note that the simplified rational function has cancelled all
factors common to both the numerator and denominator. |
| The
existence of the horizontal asymptote
is related to the degrees of both polynomials in the numerator
and the denominator of the given rational function. |
| Horizontal
asymptotes occur when either, the degree of the numerator is
less then or equal to the degree of the denominator. |
In
the case when the degree (n)
of the numerator is less then the degree (m)
of the denominator, the x-axis
y = 0
is the asymptote. |
| If
the degrees of both polynomials, in the numerator and the
denominator, are equal then, y
= an / bm
is the horizontal asymptote, written as the ratio of their
highest degree term coefficients respectively. |
| When
the degree of the numerator of a rational function is greater
than the degree of the denominator, the function has no
horizontal asymptote. |
| A
rational function will
have a slant (oblique) asymptote
if the
degree (n)
of the numerator is exactly one more than the degree (m)
of
the denominator that is if n
= m + 1. |
| Dividing
the two polynomials
that form a rational
function, of which the
degree
of
the numerator pn
(x)
is exactly
one more than the degree of the denominator qm
(x),
then |
| pn
(x)
= Q (x) · qm (x) + R
=>
pn (x) / qm (x) = Q
(x)
+ R / qm (x) |
| where,
Q (x)
=
ax + b
is the quotient and R
/ qm(x)
is the remainder with constant R. |
| The
quotient Q
(x)
=
ax + b
represents the equation of the slant asymptote. |
| As
x
approaches
infinity (or negative infinity),
the remainder R /
qm (x)
vanishes (tends to zero). |
| Thus,
to find the equation of the slant asymptote, perform the long
division and discard the remainder. |
| The
graph of a rational function will never cross its vertical
asymptote, but may cross its
horizontal or slant asymptote. |
|
| The
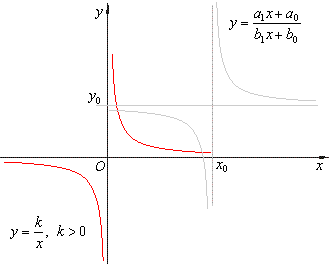
graph of the reciprocal
function, equilateral or rectangular hyperbola |
| The
graph of the reciprocal function y =
1/x or y = k/x
is a rectangular (or
right) hyperbola of which asymptotes are the coordinate axes. |
| If
k > 0
then, the function is decreasing from zero to negative infinity
and from positive infinity to zero, i.e., the graph of the
rectangular hyperbola opening in the first and third quadrants
as is shown in the right figure. |
| The
vertices, |
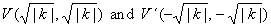 |
|
|
|
 |
|
|
|
Translation of the reciprocal function, linear rational
function |
| The
rational function |
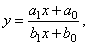 |
by
dividing the numerator by denominator, |
|
| can
be rewritten into |
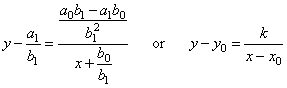 |
where, |
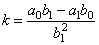 |
|
| is
the constant, |
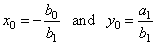 |
are
the vertical and the horizontal asymptote respectively. |
|
|
Therefore, the values of the vertical and the horizontal asymptotes
correspond to the coordinates of the horizontal and the
vertical translation of the reciprocal function y = k/x
as is shown in the figure
below.
|
 |