|
|
The
translated
cubic function |
|
Graphs
of the source and translated
cubic functions
|
|
|
|
|
|
|
|
|
| The
translated
cubic function |
| The
general cubic function y
=
a3x3
+ a2x2
+ a1x
+ a0
or
y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0), |
 |
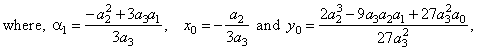| by
setting x0
=
0 and y0
= 0 we get
the source cubic function
y
= a3x3
+
a1x
where a1=
tan at
. |
|
|
| Graphs
of the source and translated
cubic functions |
| type
1 |
y
=
a3x3
+ a2x2
+ a1x
+ a0 or
y
-
y0
= a3(x
-
x0)3-
x0)3
where, |
|
 |
 |
|
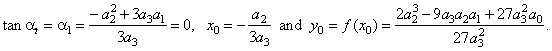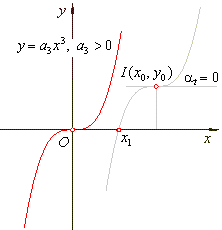The
root |
 |
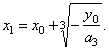The point of inflection I
(x0,
y0). |
|
|
|
|
| type
2/1 |
y
=
a3x3
+ a2x2
+ a1x
+ a0 or
y
-
y0
= a3(x
-
x0)3
+ a1(x
-
x0),
a3
· a1
>
0, |
|
 |
 |
 |
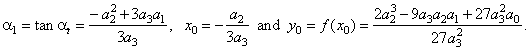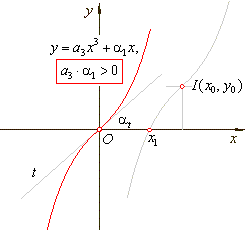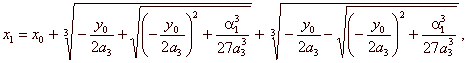I
(x0,
y0). |
|
|
|
| |
| type
2/2 |
y
=
a3x3
+ a2x2
+ a1x
+ a0 or
y
-
y0
= a3(x
-
x0)3
+ a1(x
-
x0),
a3
· a1
<
0, |
|
|
 |
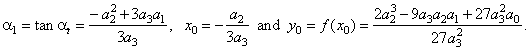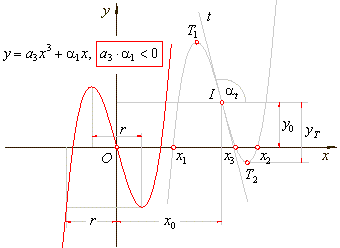| If
| y0
| > |
yT
|
|
|
| |
|
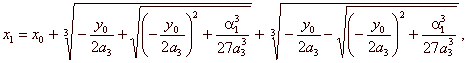| if
| y0
| < |
yT
| |
 |
|
 |
|
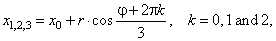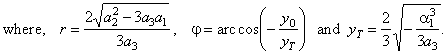The turning points |
 |
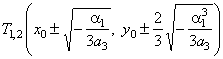The
point of
inflection
I
(x0,
y0). |
|
|
|
|
|
|
| The
graphs of
the translated cubic functions are symmetric about its
point of inflection. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
D |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
