|
|
 The
cubic
function
The
cubic
function |
|
General or translated form of cubic function |
|
Graphs
of the source cubic functions |
|
|
|
|
|
|
|
| The
cubic
function |
| General
or translated form of cubic function |
| The
general cubic function y
=
a3x3
+ a2x2
+ a1x
+ a0
or
y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0), |
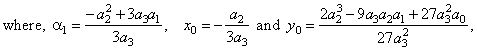 |
| by
setting x0
=
0 and y0
= 0 we get
the source cubic function
y
= a3x3
+
a1x
where a1=
tanat
. |
|
|
| There are three types
(shapes of graphs) of cubic
functions whose graphs of the source functions are shown in the figure below: |
| type
1 |
y
=
a3x3
+ a2x2
+ a1x
+ a0
or y
-
y0
= a3(x
-
x0)3,
-
a22
+ 3a3a1
= 0 or a1
= 0. |
|
| therefore,
its source function y
=
a3x3,
and the tangent line through the point of
inflection is horizontal. |
| type
2/1 |
y
=
a3x3
+ a2x2
+ a1x
+ a0
or
y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0),
where a3a1>
0 |
|
| whose
slope of the tangent line through the point of inflection is
positive and equals a1. |
| type
2/2 |
y
=
a3x3
+ a2x2
+ a1x
+ a0
or
y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0),
where a3a1<
0 |
|
| whose
slope of the tangent line through the point of inflection is
negative and is equal a1. |
| The
graph of its source function has three zeros or roots at |
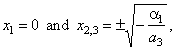 |
|
| and two turning
points at |
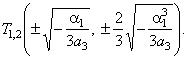 |
|
| Graphs
of the source cubic functions |
|
|
|
| Coordinates
of the point of inflection coincide with the coordinates of
translations, i.e., I
(x0,
y0).
|
| The source cubic functions are
odd functions. |
| Graphs of odd functions are
symmetric about the origin that is, such functions change
the sign but not absolute value when the sign of the independent variable is
changed, so that f
(x)
=
- f
(-x). |
| Therefore,
since f (x)
= a3x3
+
a1x
then - f
(-x)
= - [a3(-x)3
+
a1(-x)]
= a3x3
+
a1x
=
f (x). |
| That
is, change of the sign of the independent variable of a function
reflects the graph of the function about the y-axis,
while change of the sign of a function reflects the graph of the
function about the x-axis. |
| The
graphs of
the translated cubic functions are symmetric about its
point of inflection. |
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
D |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |