| |
| Algebraic
Expressions |
| |
|
|
Factoring
and expanding algebraic expressions, rules for transforming algebraic
expressions |
|
Using a variety of methods including combinations of the above to factorize
algebraic expressions |
|
|
|
|
|
|
|
|
|
| Factoring and
expanding algebraic
expressions, rules
for transforming algebraic
expressions |
| Expanding algebraic
expressions |
| The
square of a binomial, a perfect square trinomial |
|
(a +
b)2 = a2
+ 2ab
+
b2 |
|
|
(a
- b)2 =
a2
- 2ab
+
b2 |
|
|
|
| The
square of a trinomial |
|
(a - b
+
c)2 = a2
+ b2
+ c2
- 2ab
+ 2ac
- 2bc |
|
|
|
| The
cube of a binomial |
|
(a + b)3
= a3 + 3a2b
+
3ab2
+ b3 |
|
|
(a - b)3
= a3
- 3a2b
+
3ab2
- b3 |
|
|
|
| The binomial expansion
algorithm - the binomial theorem |
|
|
|
| Factoring algebraic
expressions |
| Difference of
two
squares |
|
x2
- y2
= (x - y)
·
(x
+
y) |
|
|
|
|
Sum and difference of cubes |
|
x3 - y3
= (x - y)
·
(x2
+ xy
+ y2) |
|
|
x3 +
y3
= (x + y)
·
(x2 - xy
+ y2) |
|
|
|
| The
sum and/or difference of any two numbers raised to the same
(positive integer) power |
|
x4
- y4
= (x - y)
·
(x3 + x2y
+ xy2
+ y3)
=
(x2
- y2)
·
(x2 +
y2) |
|
|
 |
|
|
|
|
|
|
|
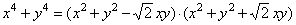x2n
- y2n
= (x - y)
·
(x2n-1 + x2n-2y
+ ¼
+ xy2n-2
+ y2n-1)
= (xn
- yn)
·
(xn +
yn) |
|
|
 |
|
|
|
|
|
|
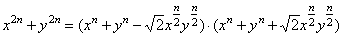| Factoring
quadratic trinomials |
| ax2
+ bx
+ c
= a·[x2
+ (b/a)·x
+ c/a]
= a·(x
-
x1)(x
-
x2), |
where
x1
+ x2
= b/a
and x1·
x2
= c/a |
|
|
| Using
a variety of methods including combinations of the above to
factorize algebraic expressions |
|
Examples:
|
|
a) x2
- 2xy
+ y2
+ 2y
- 2x
=
(x
- y)2
- 2(x
- y)
=
(x
- y)(x
- y
- 2), |
|
|
|
|
|
|
b) x2
- y2
+ xz
- yz
=
(x
- y)(x
+ y)
+ z(x
- y)
= (x
- y)(x
+ y
+ z), |
|
|
|
|
|
c) 4x2
- 4xy
+ y2
- z2
= (2x - y)2
- z2
=
(2x
- y
- z)(2x
- y
+ z), |
|
|
|
| d) a3
- 7a
+ 6
= a3 - a
- 6a
+ 6
= a(a2 -1)
- 6(a
-1)
= (a -1)·[a(a
+ 1)
- 6]
= (a -1)(a2
+ a
- 6)
= |
|
= (a -1)(a2
+ 3a
- 2a
- 6)
= (a -1)[a(a
+ 3)
- 2(a
+ 3)]
= (a -1)(a
+ 3)(a
- 2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus
contents A |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
