|
|
|
Cramer’s
rule (using the determinant) to solve systems of linear equations
|
|
Solving system
of two equations in two unknowns
using
Cramer's rule
|
|
A system of two equations in two unknowns, the solution to a system
by Cramer’s rule (use of determinants).
|
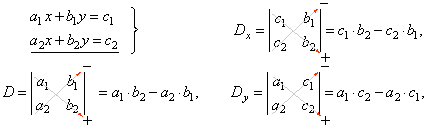
|
|
the solution to the system |
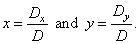 |
|
|
|
|
| Example:
Solve given system of
linear equations using
Cramer’s rule.
|
| Solution: |
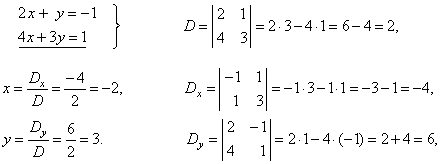 |
|
|
|
|
Solving system of three equations in three unknowns
using
Cramer's rule
|
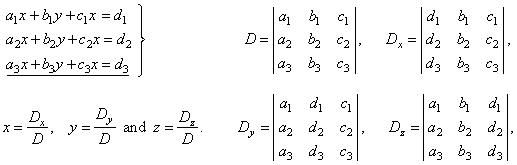
|
| A determinant of rank
n
can be evaluated by expanding to its cofactors of rank
n -
1, along any row or column taking into account the scheme of
the signs.
|
 |
|
|
| For example,
the determinant of rank
n = 3,
|
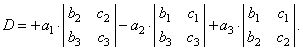 |
|
|
|
|
| Example:
Solve given system of
three equations in three unknowns using method of expanding to
cofactors.
|
| Solution: |
 |
|
|
|
|
Method of expanding
a determinant
of a rank n
by
cofactors, example
|
|
The value of a determinant will not change by adding multiples of
any column or row to any other column or row. This way created are zero entries that simplify subsequent calculations.
|
|
|
|
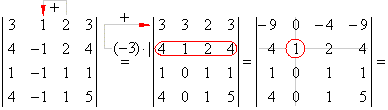
Example:
An application of the method of expanding a determinant to
cofactors to evaluate the determinant of the rank four.
|
|
|
Added is third to the second colon. Then, the second row multiplied
by -3 is added to the first row. The obtained determinant is then
expanded to its cofactors along the second colon:
|
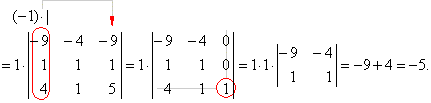
|
|
The first colon multiplied by
-1 is added to the third colon. The
obtained determinant is then expanded along the third colon.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Matrices, determinants and systems of linear equations
contents
|
|
 |
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|