|
|
| Quadratic
equation
x2
=
a,
a
>
0 |
| The quadratic equation
x2
=
a
has two solutions which are
opposite numbers only if a
> 0. |
| If
a = 0 then there is a repeated solution zero, and if
a < 0 then there are no solutions in the set of real numbers. |
| The solutions are also called the roots or zeros
of the quadratic equation. |
| Examples: |
a)
x2
= 16 |
|
b) (x
-
5)2
= 49 |
| |
x2
-
42 =
0 |
|
(x
-
5)2
-
72 =
0 |
| |
(x
-
4)
· (x
+
4) =
0 |
|
[(x
-
5) -
7] ·
[(x
-
5) +
7]
=
0 |
| |
x
-
4 =
0
=> x1
= 4 |
|
(x
-
5) -
7 =
0
=> x1
= 12 |
| |
x
+
4 =
0
=> x2
= -
4 |
|
(x
-
5) +
7 =
0 => x2
= -2 |
|
|
|
| Square
root |
| The
principal square root of a
nonnegative real number
a,
denoted |
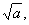 |
represents the
nonnegative real |
|
| number
x
whose square (the result of multiplying the number by itself) is
a,
that is |
|
|
|
The number a
under the root sign is called the radicand.
|
|
As the square root is defined only
when its radicand is a
nonnegative number therefore,
|
| for
example, the expression |
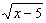 |
makes sense only if
x
-
5
>
0, that is,
only if x
>
5. |
|
|
Since the
positive square root of a positive real number is called the
principal square root this is why the square root of say 16, is
taken as +4 despite the fact that the square of -4
is also
16.
|
|
That is, by the square
root of a,
where a is
a nonnegative number, we should mean, the positive square root of
a.
|
| The
reason for taking the principal square root as the
value of a square root of a positive real number, lies
in the definition of a function f
which requires that for each x
in the domain there is at most one pair (x,
y)
in the codomain (where a set of ordered pairs (x,
y)
represents the graph of the function f
). |
|
| As
a2
> 0 whether
a
> 0 or
a
< 0 we write
|
|
|
| Examples: |
|
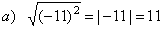 |
| |
|
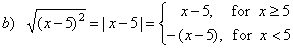 |
|
|
| Properties
of square roots |
|
|
|
| Adding,
subtracting, multiplying and dividing square roots |
|
|
|
| Rationalizing
a denominator |
| Rationalizing a denominator is a method for changing an irrational denominator into a rational one. |
|
|
| To
rationalize a denominator or numerator of the form |
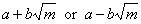 |
multiply both numerator |
|
| and denominator by a
conjugate, where |
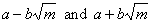 |
are conjugates of each other. |
|