|
|
|
| The
graph of the quadratic function
f
(x)
= x2 |
| A function that to every real number associates its square is called
a quadratic function and is denoted |
| f
(x)
= x2,
x
Î
R.
The point P(x,
x2)
lies on the graph of a quadratic function called a parabola. |
|
|
For
x
=
0 function
f
(x)
= x2
has minimal value f
(0)
=
02 =
0.
This point is called the turning point or the
vertex of the parabola.
|
| The
curve is symmetrical about the y-axis and has its vertex
V
(0,
0) at the origin. |
| The curve is decreasing for
x < 0 and is increasing for
x
> 0. |
| If
y
=
f
(x),
then y
=
-
f
(x)
is its reflection about the x-axis. |
| Therefore,
the graph of the quadratic f
(x)
= -x2
has its maximum at the vertex. |
| The curve is
increasing for
x < 0 and is decreasing
for x > 0. |
|
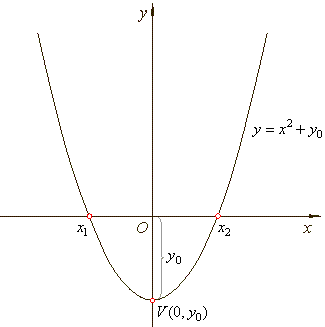
| Translation
(or shift) of the source quadratic function in the direction of
the y-axis, quadratic
function of the form f
(x)
= x2 +y0 |
| Translating
the graph of the source quadratic function vertically by y0,
the vertex of the function moves to the point V
(0,
y0 ). |
| The
translation or shift is in the positive direction of the y-axis
(upward) if y0
> 0, in the negative direction (downward) if y0
< 0. |
 |
|
| Points
where a graph crosses or touches the x-axis
are called x-intercepts,
roots or zeros. At the x-intercept
y
= 0. |
| To
find the zeros of the quadratic function, set the function equal
to zero, f
(x)
= 0,
and solve for x. |
| That
is, solve the equation x2 + y0
= 0, |
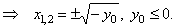 |
|
|
| Quadratic
equation
x2
=
a,
a
>
0 |
| If
a
> 0 then the quadratic equation
x2
=
a
has two solutions, |
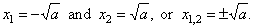 |
|
| If a
= 0 then the
equation has zero as the double root, and if a
< 0 then the equation has no real roots. |
|
|
|
| The principal square root function
- the inverse of the square of x
(or quadratic) function |
| Definition
of the inverse function |
| The
inverse function is a function, usually written f
-1,
whose domain and range are respectively the range |
| and
domain of a given function f,
that is |
| |
f
-1(x)
= y if
and only if f
(y)
= x, |
|
|
| or it is
the function whose composition with the given function
is the identity function, i.e., |
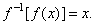 |
|
|
|
|
|
|
|
| In
order that the inverse should have a unique value for each
argument, and so be properly a function, |
| the
extraction of positive square roots
is the inverse of squaring, since |
|
|
| however,
without the restriction to positive values, the square root
function on the domain of real numbers does not have an inverse. |
|
| The
graph of the principal square root function |
| The
graph of the inverse function is the reflection about the line y =
x
of the graph of a given function. |
| A
function f has an inverse if and only if when its graph is
reflected about the line y =
x, the result is the graph of a
function that passes the vertical line test. |
| A
relation is a function if there are no vertical lines that
intersect the graph at more than one point. |
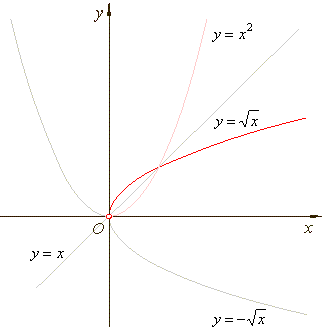 |
|
| Translation of the principal square root function
in the direction of
the x-axis |
| Horizontal
line test |
| A
function f
has an inverse if no horizontal line intersects the graph of f
more than once. |
| If
any horizontal line intersects the graph of f
more than once, then f
does not have an inverse. |
| A
mapping associating a unique member of the codomain with every
member of the domain of a function is called one to one
correspondence. |
| A
function f
is one-to-one if and only if f
has an inverse. |
| Given
f
(x)
= x2 + y0
and,
since f
[f
-1(x)]
= x |
|
therefore, f
[f
-1(x)]
= [f
-1(x)]2
+ x0
= x, or
[f
-1(x)]2
= x -
x0
|
| then |
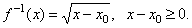 |
|
|
| To find the
y-intercept,
set x
= 0 and solve for y, that is, |
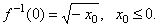 |
|
|
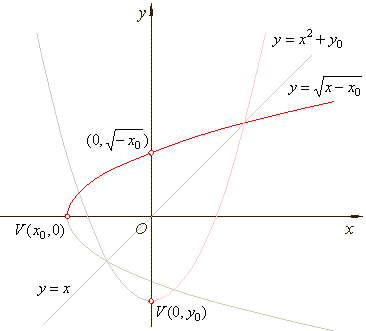
| The
graph of
translated principal square root function
in the direction of
the x-axis |
 |
|
|