|
|
|
|
Imaginary
and Complex Numbers |
 Imaginary
numbers basic definitions
Imaginary
numbers basic definitions |
|
Imaginary unit |
 Complex numbers
Complex numbers |
|
Real and imaginary
parts |
|
The complex plane |
|
The set of all complex
numbers C |
|
Absolute value,
modulus of a complex number |
|
Complex conjugates |
 Addition and
subtraction of complex numbers
Addition and
subtraction of complex numbers |
 Multiplication
and division of complex numbers
Multiplication
and division of complex numbers |
|
|
|
|
|
|
| Imaginary
numbers basic definitions |
| Imaginary
numbers are introduced to enable us to take the square root of
negative numbers. |
| Thus, for
example |
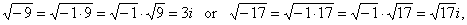 |
|
so, the square roots of negative numbers are called imaginary
numbers since they do not lie on the real number line. |
| Therefore,
the square of any imaginary number (except 0) is a negative
number. |
| That
is, any number
of the form |
| |
yi,
where |
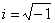 |
-
the imaginary unit and y
is any real number, |
|
| we call imaginary
number. |
| By using
the definition derived are powers of the imaginary unit i: |
|
|
| note that the powers of
i
repeat in a cycle, so that |
|
|
|
| Examples:
Reduce, i15,
i26
and i149. |
| Solutions:
i15
= i4
· 3 · i3 = i3
= -i,
i26
= i4
· 6 · i2 = i2
= -1
and i149
= i4
· 37 · i = i. |
|
| Complex numbers |
| A complex
number is the sum of a real number and an imaginary number. |
| A complex
number z
is written in the form of z
= x
+ yi,
where x
and y
are real numbers, and |
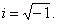 |
|
| The real
number x
is called the real part of the
complex number, and the real number y
is the imaginary part. |
| The real
part of z
is denoted Re(z)
=
x
and the imaginary part is denoted
Im(z)
=
y. |
| Hence, an imaginary
number is a complex number whose real part is zero, while real
numbers may be considered to be complex numbers with an
imaginary part of zero. |
| That is,
the real number x
is equivalent to the complex number x
+ 0i. |
| Equality
of complex numbers |
| Two
complex numbers are equal if their real parts are equal and
their imaginary parts are equal. |
|
| The
complex plane |
| Complex
numbers are represented by points or position vectors in the
coordinate plane called the complex plane (or the Gauss plane).
Where, the x-axis
is called the real axis and the y-axis
is called the imaginary axis. |
| The
representation of a complex number by Cartesian coordinates is
called the rectangular form or algebraic form of the complex
number. |
| The
standard symbol for the set of all complex numbers is C. |
|
|
|
| Absolute value,
modulus of a complex number |
| The
absolute value of a complex number z
is defined as the distance
from z
to the origin in the complex |
| plane,
i.e., |
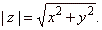 |
|
|
|
| Complex conjugates |
| The
complex conjugate of the complex number z
= x
+ yi
is x
-
yi
that has the same real part x,
but differ in the sign of the imaginary part. |
| That is,
the conjugate is the reflection of z
about the real axis,
as is shown in the above figure. |
|
| Addition and
subtraction of complex numbers |
| To add or
subtract two complex numbers z1
= a + bi
and z2
= c + di, we add or subtract the real parts
and the imaginary parts. |
| Addition: |
z1 +
z2
= (a + bi) + (c + di) = (a
+ c) + (b + d)i |
|
|
| Subtraction: |
z1
-
z2
= (a + bi) -
(c + di) = (a -
c) + (b -
d)i |
|
|
|
| Examples: Given
are complex numbers, z1
= -3 +
2i and
z2
= 4 + 3i,
find z1 +
z2 and
z1
-
z2.
|
|
Solutions:
z1 +
z2
= (-3 +
2i) + (4 + 3i) =
(-3 +
4) + (2 + 3)i = 1 + 5i
|
|
and
z1
-
z2
= (4 + 3i) -
(1 + 5i) =
(4 -
1) + (3 -
5)i =
3 -
2i |
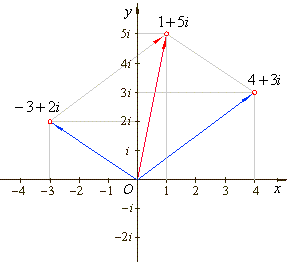
| Given
addition and subtraction are shown in the complex plane in
the figures below. |
| z1 +
z2
=
(-3 +
2i) + (4 + 3i) = 1 + 5i |
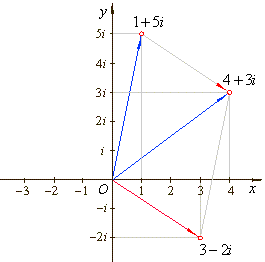
|
z1
-
z2
=
(4 + 3i) -
(1 + 5i) = 3 -
2i |
 |
|
 |
|
|
| Multiplication and
division of
complex numbers |
| Multiplication: |
z1·
z2
=
(a + bi) · (c + di) = ac
+ bci + adi + bdi2
= (ac -
bd) +
(ad + bc)i |
|
|
| Division: |
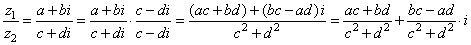 |
|
|
|
| Examples: Given
are complex numbers, z1
= -3 +
2i
and z2
= 4 + 3i,
find z1 ·
z2
and
z1
/
z2.
|
|
Solutions:
z1 ·
z2
= (-3 +
2i) · (4 + 3i) =
-3 ·
4 + 2 · 4i +
(-3)
· 3i +
2 · 3 i2
= -18
-
i
|
|
and |
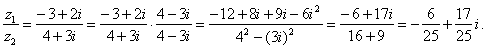 |
|
|
|
|
| Example:
For what real
number
a the real part of the complex number |
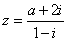 |
equals
1. |
|
|
|
Solution:
|
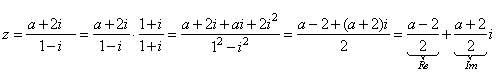 |
| |
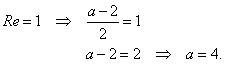 |
|
|
| Example:
Evaluate the
expression |
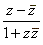 |
where
z = 1 -
i. |
|
|
|
Solution:
|
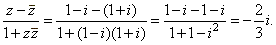 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Intermediate
algebra contents |
|
|
 |
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|