|
|
|
|
Graphing
Linear Equation, Linear Function (First Degree Polynomial)
|
The
point-slope form of a line
|
|
Parallel
and perpendicular lines
|
|
General
form of the equation of a line
|
|
The two point form of the equation of a line
|
|
|
|
|
|
|
| The
point-slope form of a line
|
| The
equation of a line that passes through the given point (x1,
y1)
and has the given slope m
is represented by the
definition of the slope and is called point-slope form or the
gradient form of the line. |
| Since the slope
of a line is the ratio of its vertical change to its horizontal
change then |
 |
|
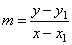or y
-
y1 = m(x
-
x1) |
| The
equation can also be considered as the translation of
the source linear function |
| y
= mx to the
point P1(x1,
y1). |
|
 |
|
|
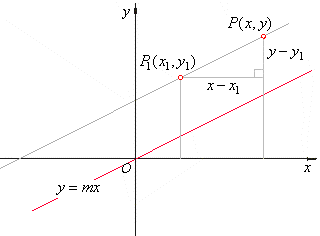| Example:
Find the equation of the line that is parallel with the line y
= - x
- 2 and passes through the point |
|
P1( 2,
1) . |
|
|
|
| Parallel
and perpendicular lines
|
| Two lines having slopes
m1
and m2
are parallel if |
| |
m1
= m2 |
|
that is, if
they have the same slope. |
|
|
| To acquire the criteria when two lines,
y
= m1x
and y
= m2x |
| are
perpendicular or orthogonal we can use the principle of similar triangles,
OA'A
and OB'B in the picture. |
| Therefore, |
m1
: 1
= -1
: m2 |
=> |
 |
|
 |
|
|
|
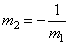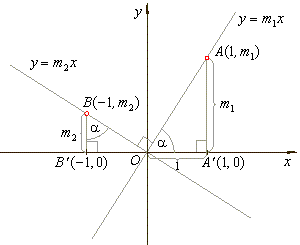| This relation will stay
unchanged if we translate the perpendicular lines, that is, when
lines |
|
y
= m1x
+ c1
and y
= m2x
+ c2
are written in the slope-intercept form. |
| Two lines are perpendicular if the slope of one line is the negative
reciprocal of the other. |
|
| Example:
Find the equation of the line that is perpendicular to the line |
 |
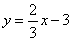and passes through |
|
|
the point A(-2,
5). |
 |
|
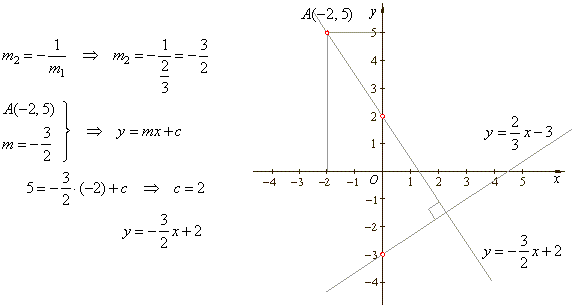| General
form of the equation of a line
|
| The linear equation
Ax +
By +
C
= 0 in two unknowns, x
and y, of
which at least one of the coefficients, A
or B, are different then zero,
is called the general form for the equation of a line. |
| Dividing the
equation by
B, where
B
is not 0, gives |
| |
 |
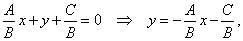where |
 |
|
|
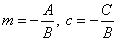| the slope-intercept form
y
= mx
+ c
of a line. |
| By putting
C
= 0 into the general form obtained is |
 |
|
|
|
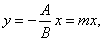the equation of the
line that passes through the origin. |
| Setting
A = 0, gives |
 |
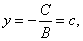the
line parallel to the x-axis. |
|
|
| And setting
B = 0 gives |
 |
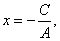the
line parallel to the y-axis. |
|
|
|
| The
two point form of the equation of a line
|
| Two points
P1(x1,
y1)
and P2(x2,
y2)
determine a unique line on the
Cartesian plane, therefore their |
| coordinates satisfy the equation
y
= mx
+ c. |
| The equation
of the line which passes through the point P1(x1,
y1)
is y -
y1
= m(x
- x1). |
| As the
point P2(x2,
y2)
lies on the same line, its coordinates must satisfy
the same equation, so |
| y2 -
y1
= m(x2
- x1)
. |
| Thus,
the slope |
 |
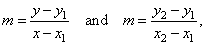| then |
 |
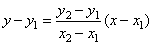| is
the equation of the line passing through the two points. |
|
|
 |
|
|
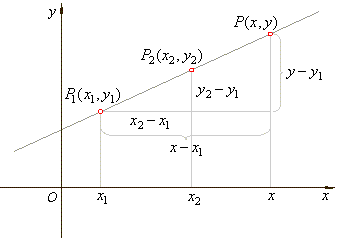| Example:
Find the equation of the line which passes through points P(-2, 3) and
Q(6,
-1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
| Intermediate
algebra contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
