|
| Conic
Sections |
|
|
|
|
Ellipse
and Line
|
Intersection of ellipse and line - tangency condition
|
|
Equation of the tangent at a point on the ellipse
|
|
Construction of the tangent at a point on the ellipse
|
|
Tangents to an ellipse from a
point outside the ellipse - use of the tangency condition
|
|
Construction of tangents from a point outside the ellipse
|
|
Ellipse and line examples
|
|
|
|
|
|
|
| Intersection of ellipse and line - tangency condition
|
| Common points of a line and an ellipse
we find by solving their equations as a system of two equations in two
unknowns, x
and y, |
|
(1) y = mx + c |
|
(2) b2x2 + a2y2
= a2b2 |
| |
|
by plugging (1)
into (2)
=>
b2x2
+ a2(mx + c)2 = a2b2 |
|
after rearranging, (a2m2
+ b2)·x2 + 2a2mc·x
+ a2c2 -
a2b2 = 0 |
| obtained
is the quadratic equation in x.
Thus, the coordinate of intersections are, |
 |
|
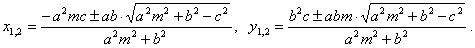Using the above solutions follows that a line and an ellipse can have one of three possible mutual positions
depending of the value of the discriminant D
= a2m2
+ b2 -
c2. Thus, if |
|
D > 0, a line and an ellipse
intersect, |
|
D = 0,
or |
a2m2
+ b2 = c2 |
a line is the tangent of the
ellipse and it is tangency
condition. |
|
|
The line touches the ellipse at the tangency point whose coordinates are: |
|
|
|
D < 0, a line and an ellipse
do not intersect. |
|
| Equation of the tangent at a point on the ellipse
|
| In the equation
of the line y
-
y1 = m(x
-
x1)
through a given point P1, the slope m
can be determined using known coordinates (x1,
y1) of the point of tangency, so |
 |
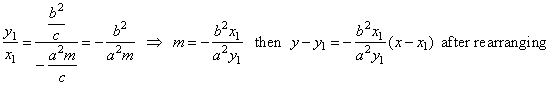| b2x1x
+ a2y1y
= b2x12
+ a2y12,
since b2x12
+ a2y12 =
a2b2
is the condition that P1
lies on the ellipse |
| |
then |
b2x1x
+ a2y1y
= a2b2 |
is the
equation of the tangent at the point P1(x1,
y1)
on the ellipse. |
|
|
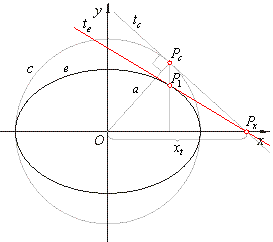
| Construction of the tangent at a point on the ellipse
|
| Draw a circle of a radius
a concentric to the ellipse. Extend the ordinate of the given point to find intersection |
|
with the circle. The tangent of the circle at
Pc
intersects the x-axis at
Px. The tangent to the ellipse at the point
P1on the
ellipse intersects the x-axis at the same point.
|
To prove this, find the
x-intercept of each tangent
analytically. |
Therefore, in both equations of tangents set y = 0 and
solve for x, |
 |
|
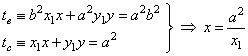it is the x-intercept of the tangent
tc
and the tangent te.
|
|
 |
|
|
| Tangents to an ellipse from a
point outside the ellipse - use of the tangency condition
|
| Coordinates of the point
A(x, y), from which we draw tangents to an ellipse, must satisfy
equations of the tangents, y
= mx + c and their slopes and intercepts,
m and
c, must satisfy the
condition of tangency therefore, using the system of equations, |
|
(1) y = mx + c
<=
A(x, y) |
|
(2) a2m2 + b2
= c2
determined are equations of the tangents from a point A(x, y)
outside the ellipse. |
|
|
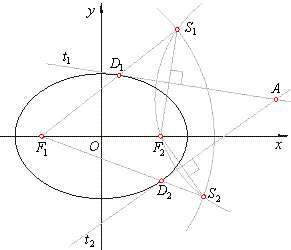
| Construction of tangents from a point outside the ellipse
|
| With
A
as center, draw an arc through F2, and from
F1
as center, draw an arc of the radius 2a. Tangents are |
|
then the perpendicular bisectors of the line segments,
F2S1 and
F2S2.
|
|
We can also draw tangents as lines through A
and the intersection points of the segments F1S1 and
F1S2
and the ellipse. |
| Thus, these intersections are the tangency points
of the tangents to the ellipse. |
| Explanation of the construction lies at the fact that, |
|
F1S1 =
F1D1 +
D1S1 =
F1D1 +
D1F2 = 2a
|
|
according to the definition of the ellipse, as well as
the point A
is equidistant from points F2 and
S1,
since the point S1
lies on the arc drawn from A
through F2.
|
|
 |
|
|
| Ellipse and line examples
|
| Example:
At a point A(-c,
y
> 0) where c
denotes the focal distance,
on the ellipse
16x2
+ 25y2 = 1600
drawn is a tangent to the ellipse, find the area of the triangle that tangent forms by the coordinate axes. |
| Solution:
Rewrite the
equation of the ellipse to the standard form 16x2
+ 25y2 = 1600 | ¸
1600 |
|
|
| We calculate the ordinate of the point
A
by plugging the abscissa into equation of the ellipse
|
| x =
-6
=>
16x2
+ 25y2 = 1600, |
|
|
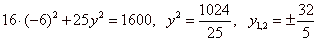
or, as we know
that the point with the abscise
x = -
c
has the ordinate equal to the value of the
semi-latus rectum,
|
|
|
 |
|
 |
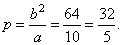
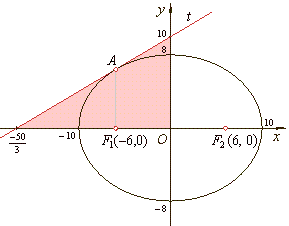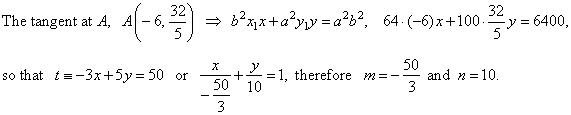| The
area of the triangle formed by the tangent and the coordinate axes, |
 |
|
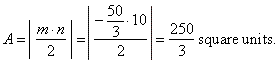| Example:
Find a point on the ellipse
x2
+ 5y2 = 36 which is the closest, and which is the farthest from the
line 6x + 5y - 25 =
0. |
Solution:
The tangency
points of tangents to the ellipse which are parallel with the given
line are, the
closest and the farthest points from the line.
|
| Rewrite
the equation of the ellipse to determine its axes, |
 |
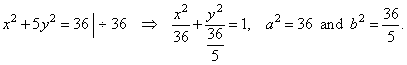| Tangents and given line have the same slope, so |
 |
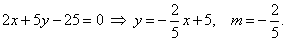| Using the tangency condition, determine the intercepts
c, |
 |
|
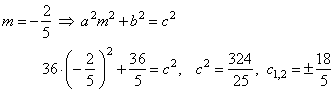therefore, the
equations of tangents,
|
|
|
 |
|
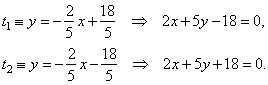
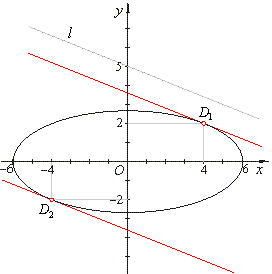
Solutions of the system of equations of tangents to the ellipse determine the points of contact, i.e., the
closest and the farthest point of the ellipse from the given line, thus |
 |
|
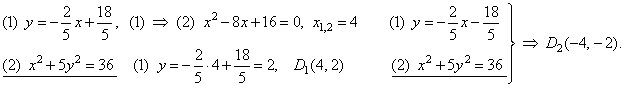| Example: Determine equation of the ellipse which the line
-3x +
10y = 25 touches at the point
P(-3,
8/5). |
| Solution:
As the given line is the tangent to the ellipse,
parameters, m
and c
of the line must satisfy the tangency condition, and the point P
must satisfy the equations of the line and the ellipse, thus |
 |
|
|
|
|
|
|
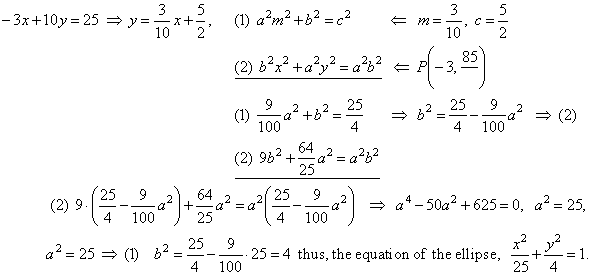