|
| Conic
Sections |
|
|
|
|
|
Ellipse
|
The parametric equations of the ellipse |
|
Equation of a translated ellipse
|
|
The equation of the ellipse examples |
|
|
|
|
|
|
| The parametric equations of the
ellipse |
| Equation of the ellipse in the explicit form |
 |
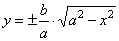can help us to explain another construction |
|
| of
the ellipse. So, in the coordinate system draw two concentric circles of radii equal to lengths of the semi axes a and b, with the center at the origin as shows the figure. |
An arbitrary chosen line through the origin intersects the
circle of the radius a
at the point R
and the circle of radius b
at M.
|
|
Then, the parallel line with the major axis through M
intersects the parallel line with the minor axis through
R, at
a point P(x,
y) of the ellipse.
Proof, |
| in
the figure, OS
= x,
PS
= y
and |
 |
|
|
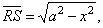as the triangles
OMN
and ORS
are similar, then
|
|
OM
: OR
= MN
: RS
or b
: a
= PS
: RS,
|
| so
that |
 |
|
|
 |
|
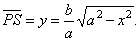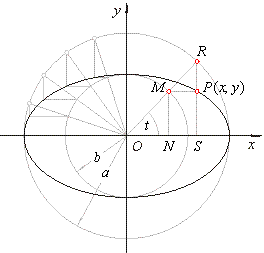| It proves that the point
P(x,
y) obtained by the construction
lies on the ellipse. This way, using the figure, we also derive |
| the
parametric equations of
the ellipse |
 |
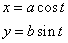where the parameter
t
is an angle 0
<
t
<
2p. |
|
| By dividing the first parametric equation by
a
and the second by b, then square and add them, obtained is
standard equation of the ellipse. |
|
| Equation of a translated ellipse
-the ellipse with the center at
(x0,
y0)
and the major axis parallel to the x-axis. |
| The equation of an ellipse that is translated from its standard position can be obtained by replacing
x
by x0 |
| and
y by
y0 in its standard equation, |
 |
|
|
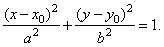| The above equation can be rewritten into
Ax2
+ By2 + Cx + Dy + E = 0. |
| Every equation of that form represents
an ellipse if A
not equal
B
and A ·
B > 0 that is, if the square terms have unequal coefficients, but the same
signs. |
|
| The
equation of the ellipse examples |
| Example:
Write equation of the ellipse passing through points
A(-4,
2) and B(8,
1). |
| Solution:
Given points must satisfy equation of the ellipse, so |
 |
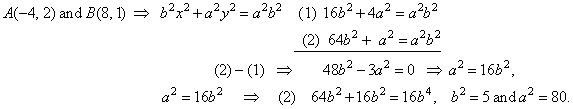| Therefore,
the equation of the ellipse |
 |
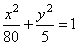or
x2
+ 16y2 = 80. |
|
|
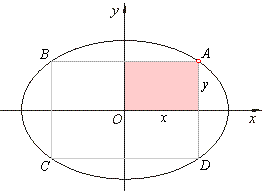
| Example:
In the ellipse 4x2
+ 9y2 = 144 inscribed is a rectangle whose vertices lie on the ellipse and
whose sides are parallel with ellipse axes. Longer side, which is parallel to the major axis, relates to the shorter
side as 3 :
2. Find the area of the rectangle. |
| Solution: It follows from the given condition that the coordinates
of vertices of the rectangle must satisfy the |
|
same ratio, i.e.,
x :
y
= 3 :
2
=>
x =
3y/2.
|
| To determine points of the ellipse of which coordinates are in this ratio, put these variable
coordinates into equation of the ellipse, |
| P(3y/2,
y) =>
4x2
+ 9y2 = 144 |
|
4(3y/2)2
+ 9y2 = 144 =>
18y2 = 144,
|
|
y1,2 =
±Ö144/18 =
±2Ö2,
x =
3y/2
=>
x1,2 =
±3Ö2.
|
|
Therefore, the vertices of the rectangle,
|
|
 |
|
| A(3Ö2,
2Ö2),
B(-3Ö2,
2Ö2),
C(-3Ö2,
-2Ö2)
and D(3Ö2,
-2Ö2). |
| The
area of the rectangle A =
4 ·
x
·
y =
4 ·
(3Ö2
)
· (2Ö2
)
=
48 square units. |
|
| Example:
Given is equation of the ellipse
4x2
+ 9y2
+ 24x -18y
+ 9 =
0,
find its center S(x0,
y0),
the semi-axes and intersections of the ellipse with the coordinate axes. |
| Solution: Coordinates of the center and the semi-axes are shown
in the equation of the translated ellipse, |
|
|
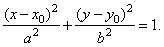
| Rewrite the given equation to that
form, |
| 4(x2
+ 6x)
+ 9(y2 -
2y)
+ 9 = 0 |
|
4[(x
+ 3)2 -
9] +
9[(y -1)2
-1]
+ 9 = 0
|
|
4(x + 3)2
+ 9(y -1)2
= 36
or
|
|
|
 |
|
|
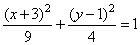
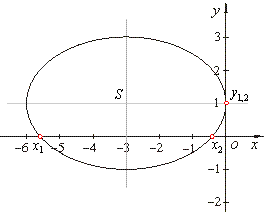
therefore,
S(-3,
1),
a = 3 and
b = 2.
|
|
Intersections of the ellipse and the
x-axis
we obtain by setting y =
0 into the equation of the ellipse, thus
|
| 4x2
+ 24x + 9 =
0,
x1,2 = -3
± 3Ö3/2, |
| and intersections of the ellipse
with the y-axis by
setting x
= 0, =>
9y2
-18y
+ 9 =
0,
y1,2 = 1. |
|
|
|
|
|
|
