Solid figures solved problems, Prisms and pyramids

Geometry - solid figures solved problems

Solid figures, solved problems examples

Example: The midpoint of the altitude of a tetrahedron of the edge a is connected with all three vertices of the base, find the angle these connections make.

Solution: Given a. a = ?

Example: Given is a cube of edge a. Midpoints of its faces are vertices of a regular octahedron. Find the volume of the octahedron.

Solution: Given a. V_octahedron = ?

Example: By rolling the cone about its apex obtained is lateral surface area of a cone in a form of a semicircle of radius R = 2Ö3 m. Find the volume of the cone.

Solution: Given R = 2Ö3 m. V_cone = ?

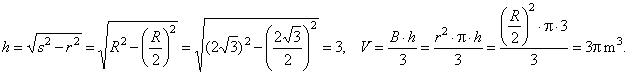Example: Volume of a circular cone is V. Through the midpoint of the altitude of the cone passes a plane parallel to the base of the cone, find the volume of the part of the cone between base and the plane.

Solution: Given V. V_{conical
frustum} = ?

Example: In a cone of base B and the height h inscribed is a cone with the vertex at the center of the given cone and whose height is half of the given cone. Find the volume of the inscribed cone.

Solution: Given B and h. V_{inscribed cone} = ?

Example: An isosceles triangle, of leg b = 2 that is inclined to the base at a = 30°, rotates around its base bisector. Find the volume of obtained solid of revolution.

Solution: Given b = 2 and a = 30°. V_{solid
of revolution} = ?

Example: Find the volume of the solid generated by rotating an equilateral triangle ABC of the side a = 2 around the axis which passes through vertex C parallel to base AB.

Solution: Given a = 2. V_{solid
of revolution} = ?

Example: In a regular square pyramid of height 2 and side of the base 1 inscribed is a cube. The side of the cube is?

Solution: Given h = 2 and a = 1. x = ?

Example: Height of a cone is 12 and the volume 324p. Find the central angle of the sector to which is unrolled the side surface of the cone.

Solution: Given h = 12 and V = 324p. a = ?

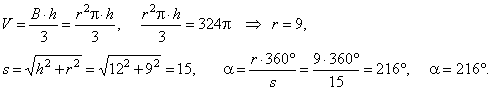Geometry and use of trigonometry contents - B