|
| Quadrilaterals,
Polygons - Regular Polygons, Circle |
|
|
|
Circle
|
 Central angle, inscribed angle
Central angle, inscribed angle
|
 Construction of a tangent
from a point
Construction of a tangent
from a point
|
 Circumference, length of an arc
Circumference, length of an arc
|
 Circle and circular sector
Circle and circular sector
|
 Circular segment
Circular segment
|
 Annulus and annulus segment
Annulus and annulus segment |
|
|
|
|
|
|
| Circle
|
| A circle is a set of points that are at the fixed distance (called the
radius r) from a fixed point called the center
O. |
|
| Central angle, inscribed angle
|
| A
central angle is
double the inscribed angle (formed when two secant lines intersect
on the circle) subtended by the same arc. |
| Proof:
Angles
b1
and b2 are
external angles of the isosceles triangles AOC and
BOC, hence |
| b1
= 2a1,
b2
= 2a2,
a
= a1+
a2
=>
b = b1+
b2
= 2(a1+
a2)
= 2a |
|
|
| Inscribed angles
subtended by the same arc are equal. An angle inscribed in a semicircle is a right angle. |
|
| Construction of a tangent
from a point P
to a circle c. |
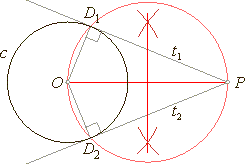 |
The
midpoint of the line segment OP
is the circumcenter of the quadrilateral PD1OD2.
The lines PD1
and PD2
are tangents from P
to the given circle c. |
|
|
| Circumference, the length of a circle - the perimeter:
|
|
 |
|
|
| Length of an arc:
|
|
|
|
| Circle and circular sector
|
| By substituting
P = 2pr
and R
= r
in the formula for the area of a regular polygon, obtained is the formula
for the area of a circle, that is : |
|
|
|
| Circular segment
|
| The portion of a circle bounded by an arc and a chord is called a segment. |
| Symbols
used in the formulas: c
-chord, r
-radius, h
-height of a segment, A
-area of a segment. |
|
|
|
| Annulus and annulus segment |
| Annulus
or ring is the region enclosed between two concentric circles. |
| Annulus |
Annulus
segment |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Geometry
and use of trigonometry contents - A |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |