|
| Applications
of Trigonometry |
|
 Applications
of Trigonometry in Solid Geometry
Applications
of Trigonometry in Solid Geometry |
 Right and
regular pyramids
Right and
regular pyramids |
|
Pyramids, examples |
 Sections of solids
Sections of solids |
|
Sections of solids, examples |
|
|
|
|
|
|
|
|
|
Applications
of trigonometry in Solid Geometry
|
|
Right and regular pyramids
|
|
A pyramid is a polyhedron with one polygonal face, the base, (not necessarily a regular polygon) and all
lateral faces triangular with a common vertex (apex).
|
|
A right pyramid is a pyramid for which the line joining
the centroid of the base (the point of coincidence of the medians) and the apex is perpendicular to the base.
|
|
A regular pyramid is a right pyramid whose base is a regular polygon and the other faces are congruent
isosceles triangles. Note that,
|
|
- if all lateral edges of a pyramid form equal angle with the
base then,
|
|
a)
all lateral edges are equal,
|
|
b)
the pyramid’s altitude foot is the center
of the circumcircle of the base.
|
|
- If all lateral faces of a pyramid form the same face-to-base dihedral
angle then,
|
|
a)
the slant heights of all faces are equal,
|
|
b)
the pyramid’s altitude foot is the center of the
incircle,
|
|
c)
B
= Slat. · cosa,
where B
is the area of the base and Slat.
is the lateral surface area.
|
| Thus, for example in the regular pentagonal pyramid
shown in the
|
| right
figure,
|
| h
= s · sina
and r
= h · cota,
then the area of the DABO |
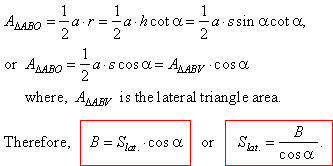 |
|
 |
|
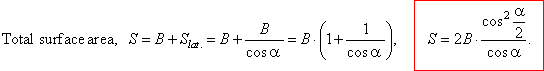
|
|
|
| Pyramids,
examples |
| Example:
Known is surface area of a regular triangular pyramid
S
and given is the base-to-face angle a,
determine the base edge a. |
| Solution: Using above formula for the surface area of a regular pyramid, |
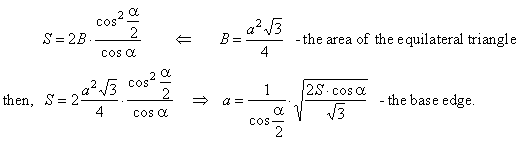
|
|
|
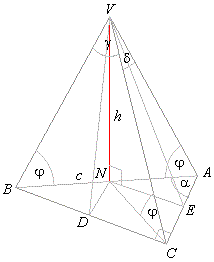
| Example: The base of a pyramid is a
right triangle with hypotenuse
c
and the acute angle a, and lateral
edges incline to the base at the same angle j, see
the down figure. Determine the volume of the pyramid and
angles of the lateral faces at the pyramid vertex. |
| Solution: Since lateral edges incline to the base at the same
angle,
lateral edges are the same length, and the foot of the
pyramid’s
altitude is the center of the circumcircle. |
| In a right triangle the center
of the circumcircle is the midpoint of the hypotenuse. |
| Hence, line segments,
AN,
BN
and CN
are the projections of the lateral edges to the plane of base, and thus the
angles, |
| angle
VNB =
angleVCN =
angle VAN = j |
| The
volume of the pyramid, |
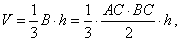 |
|
 |
|
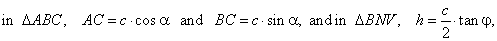
|
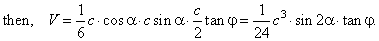
|
|
Denote the angles of lateral faces at the pyramid
vertex, angle
AVB =
b,
BVC =
g
and angle
AVC =
d.
|
|
As lateral faces are isosceles triangles, their altitudes,
VD,
VE
and VN
bisect corresponding sides of the base. In DAVB,
b =
180° -
2j,
|
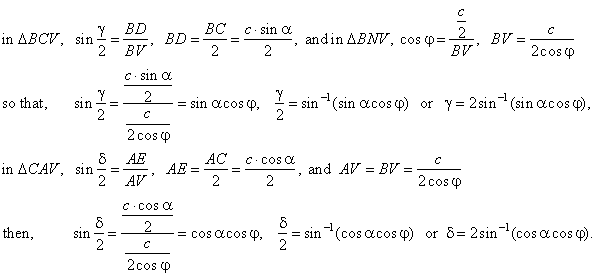
|
|
|
|
Sections of solids
|
|
Sections of solids, examples
|
|
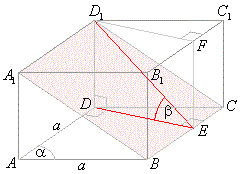
Example:
The base of a parallelepiped is a rhombus. Through an edge of the bottom base and the opposite
edge of the top base passes an intersection plane that forms with the bottom base the angle
b, as shows
the figure down. The area of the section is As. Determine the lateral surface of the parallelepiped.
|
| Solution: From the vertices
D
and D1
draw the altitudes of the top and bottom rhombus. The obtained parallelogram
EFD1D
is perpendicular to the planes of bases and intersects
the plane
in the segment ED1 that makes angle
b with
ED. |
Since bases are rhombuses, the lateral surface consists of
four equal rectangles. |
| Area of the lateral face
ADD1A1,
ALF =
A1D1
· DD1, |
|
 |
|
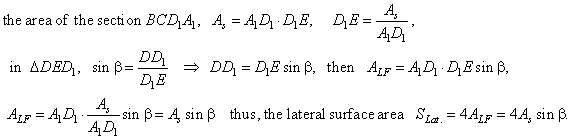
|
|
|
|
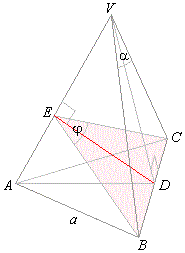
Example:
Vertex angles of faces of a regular triangular pyramid with a side of the base
a, are all equal and
denoted
a, as is shown in
the down figure. Determine face to face dihedral angles and the area of section that the plane passing through a side of the base
perpendicular to the opposite lateral edge cuts of the pyramid.
|
| Solution: All face to face angles are the same and one of them, |
| denoted
j, is shown in the diagram. |
| Section
BCE is an isosceles triangle of the area |
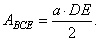 |
|
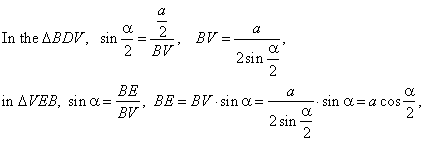 |
|
 |
|
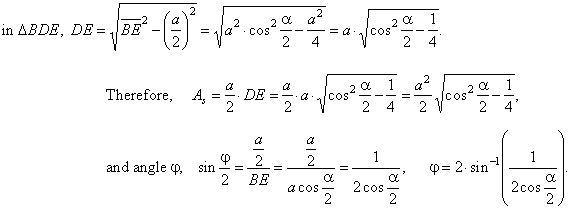
|
|
|
|
Example:
Through the vertex of a cone laid is a plane that makes the angle
j with its base and cuts the
segment bounded by arc that subtends the central angle
a, as is shown in
the below figure. The distance of
the plane from the center of the base equals
d. Determine the volume of the cone.
|
|
Solution:
Angle VOC equals angle
ODV = j since they have mutually
perpendicular sides.
|
|
|
|
|
|
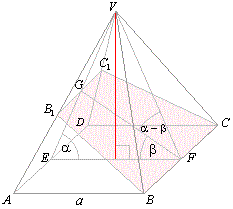
Example:
Lateral faces of a square pyramid are inclined to the base by angle
a. Through the base’s edge
laid is a plane that forms with the base of the pyramid the angle
b, as shows
the below figure. Find the area
of the section if the side of base is
a.
|
|
Solution:
Through midpoints E and
F of the two opposite sides of base
passes the plane EFV which is perpendicular to
the base and intersects the plane of the trapezoid BCC1B1
along the segment
FG (the altitude of the
trapezoid).
|
| From DEFG by
using the sine law |
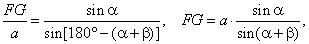 |
| and since
triangles, ADV
and
B1C1V
are similar
|
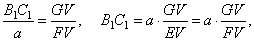 |
| where B1C1
is shorter base of the trapezoid.
|
|
 |
|
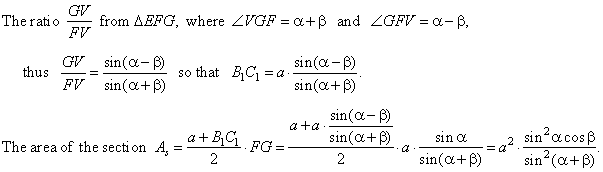
|
|
|
|
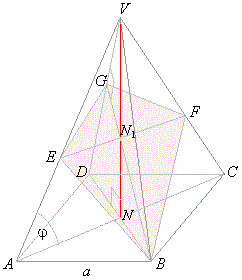
Example:
Through a vertex of the base of a square pyramid laid is a plane perpendicular to the opposite
lateral edge. Determine the area of the section if length of the side of the base is
a and if the lateral edge is inclined to base at angle
j, see
the figure down.
|
| Solution:
The section is the deltoid
EBFG with the diagonal
BG perpendicular to the lateral edge DV and the shorter diagonal
EF that
is parallel with the diagonal AC of the base. |
| Area of the section
As
= (1/2)
· BG
· EF. |
| In the right triangle
BGD, where |
| angle
GDB =
j and the
hypotenuse DB =
aÖ
2, |
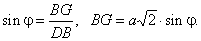 |
| In the isosceles triangle
EFV, where
angle
VEF =
j |
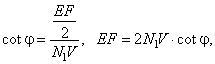 |
|
 |
|
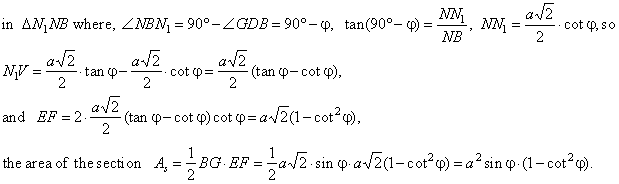
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Geometry
and use of trigonometry contents - B |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |