|
|
 Absolute value
inequalities
Absolute value
inequalities |
|
Solving
linear inequalities with absolute value |
|
Examples
of solving
linear inequalities with absolute value |
|
|
|
|
|
|
|
| Absolute value
inequalities |
| Solving
linear inequalities with absolute value |
| Graphical
interpretation of the
definition of the
absolute value of a function y =
f (x) will help us solve
linear inequality with absolute value. |
| The
definition for the absolute value of a function is given by |
|
|
| Thus,
for
values of x
for which f
(x)
is nonnegative, the graph of | f
(x) | is the
same as that of f
(x). For values of
x
for which f
(x)
is
negative, the graph of | f
(x)
| is a reflection of
the graph of f
(x)
on the x
axis. |
| That
is, the
graph of y = -
f
(x) is obtained by reflecting the graph
of y =
f (x)
across the x-axis. |
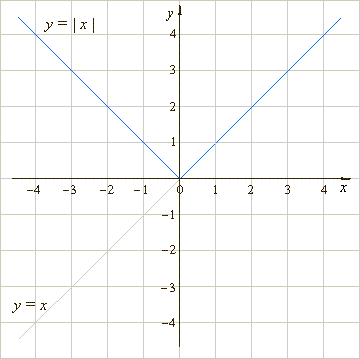
| Hence,
the graph of the absolute value of
the function
y =
x,
i.e.,
| x | is |
 |
|
| Examples
of solving
linear inequalities with absolute value |
| Example:
Solve the absolute value
inequality | x
-
2
| <
3. |
|
Solution: Graphical
interpretation of the given inequality will help us find
values of x
for which left side of the inequality is less then or equal to
3. |
| For
values of x
for which y
is nonnegative, the graph of | y
| is the
same as that of y =
x -
2.
|
| For values of
x
for which y
is
negative, the graph of | y
| is a reflection of
the graph of y
across the x
axis. |
| Since
the graph of y =
x -
2 has y
negative on
the interval (-
oo,
2 ) it is this part of the graph
that has to be reflected on the x
axis. |
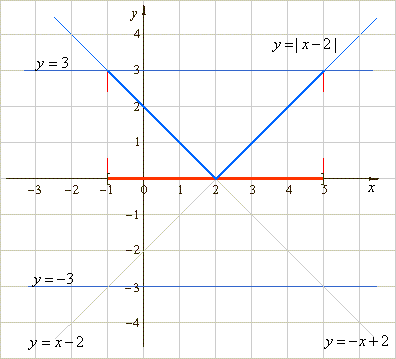 |
| The
graph shows that
values of x from
the closed interval [-1,
5] satisfy the given inequality. |
| The
same result can be obtained algebraically by solving the
compound inequality. |
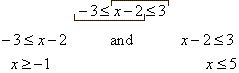 |
 |
| x
Î [-1,
5] |
|
|
|
Generally, when
solving inequalities involving the absolute value of a linear
function y =
ax+
b, we consider the two different
cases.
|
| 1)
When the initial inequality is of the form
| ax +
b |
< c
or ( | ax +
b |
< c ) |
| we
replace it by the compound inequality -
c
<
ax +
b <
c
or (-
c
< ax +
b < c). |
| Note that there are two inequalities
here and the way they are written implies that both first AND
the second inequalities must be satisfied. The solution set will
then be an intersection of two
sets, as is shown above.
|
| 2)
When the initial inequality is of the form
| ax
+
b |
> c
or ( | ax
+
b | > c) |
| we
replace it by two inequalities ax
+
b < -
c OR ax
+
b > c or
(
ax +
b
< - c
OR ax
+
b
> c) |
| The way
the two inequalities are written implies that the first OR the
second inequality must be satisfied. |
| The solution set will then
be the union of two sets, as is
shown in the example below. |
| Notice that in both cases the corresponding graph of the given inequality suggests its solution. |
|
|
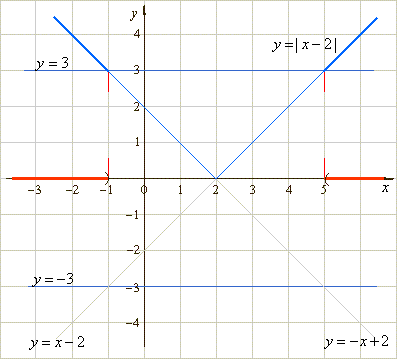
| Example:
Solve the absolute value
inequality | x
-
2
| > 3. |
|
Solution: Again, graphical
interpretation of the given inequality will help us find
values of x
for which left side of the inequality is greater than 3. |
| The
graph shows that
values of x from
the open intervals, (-
oo , -1)
or (5, oo )
satisfy the given inequality. |
|
 |
|
| The
same result can be obtained algebraically by solving the two
inequalities |
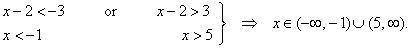 |
|
|
|
|
|
|
|
|
|
|
|
|
Functions
contents A
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |