|
|
 Absolute value
equations
Absolute value
equations |
|
Solving absolute value
equations |
 Linear Inequalities
Linear Inequalities
|
|
Solving
inequalities |
|
Properties of
inequalities |
|
Examples
of solving single linear inequalities |
|
Solving
compound (double) inequalities |
|
|
|
|
|
|
| Absolute value
equations |
| Solving absolute value
equations |
| Recall
that the absolute value of a real number a,
denoted |
a |,
is the number without its
sign and represents the distance between 0 (the origin) and that
number on the real number line. |
|
Thus, regardless of the value of a number
a
its absolute value is
always either positive or zero, never negative that is, | a
|
> 0.
|
| To
solve an absolute value equation, isolate the absolute value on
one side of the equation, and use the definition of absolute
value. |
| If the number on the other side of the equal sign is positive, we will need to set up two
equations to get rid of the absolute value, |
|
- the first equation that set the expression inside the absolute value symbol equal to the other side of the equation, |
|
- and the second equation that set the expression inside the absolute value equal to the
opposite of the number on the other side of the equation. |
| Solve
the two equations and verify solutions by plugging the solutions
into the original equation. |
| If
the number on the other side of the absolute value equation is negative then
the equation has no solution. |
|
|
Example:
|
1
- 2x
| = 17
|
|
Solution:
1
-
2x =
17
or
1 -
2
x = -17 |
|
2
x = - 16
2x =
18 |
|
x = -
8
x = 9 |
|
| The
solutions to the given equation are
x = - 8
and
x = 9. |
|
|
Example:
|
-3
- x
| = 5
|
|
Solution:
-3
-
x = 5
or
-3
-
x = -5 |
|
x = -
8
x = 2 |
|
| The
solutions to the given equation are
x = - 8
and
x = 2. |
|
|
Example:
|
x + 1 | =
2x -
3
|
|
Solution:
x + 1 = 2x
-
3
or
x + 1 = -(2
x -
3) |
|
x - 2x
= - 4
x +
2x = 3 -
1 |
|
x = 4
3x = 2
=> x = 2/3 |
|
| Check
solutions: |
| x = 4
=>
|
x + 1 | =
2x -
3,
x = 2/3
=>
|
x + 1 | =
2x -
3 |
|
|
4
+ 1 | =
2 · 4 -
3
|
2/3 + 1 | =
2 · 2/3 -
3
|
|
5 = 5
5/3 is not equal
-5/3 |
| The
check shows that x =
2/3 is not a solution,
because the right side of the equation becomes negative. There is a single solution to this equation: x = 4. |
|
|
Example:
|
x + 2 | =
| 2x -
5 |
|
|
Solution: As both
sides of the equation contain absolute values the
only way the two sides are equal is, the two quantities
inside the absolute value bars are equal or equal but with
opposite signs.
|
|
x + 2 = 2x
-
5
or
x + 2 = -(2
x -
5) |
|
x -
2x
= -
5 -
2
x + 2 = -2
x +
5 |
|
-x =
-7
3x = 3 |
|
x = 7
x = 1 |
|
| Check
solutions: |
| x =
7 =>
|
x + 2 | =
| 2x -
5 |, x = 1
=>
|
x + 2 | =
| 2x -
5 | |
|
|
7 + 2 | =
| 2 · 7 -
5
|
|
1 + 2 | = | 2 ·
1 -
5 |
|
|
9 = 9
3 = | -3 | |
|
| Therefore,
the
solutions to the given equation are x =
7 and x =
1. |
|
| Linear Inequalities
|
| A linear inequality
is one that can be reduced to the standard form
ax +
b
> 0 where a,
b
Î
R,
and where other inequality signs like <
, > and
<
can appear. |
| Solving
inequalities |
| The solutions to an inequality are all values of
x
that make the inequality true. Usually the answer is a range of
values of x
that we plot on a number line. |
| We
use similar method to solve linear inequalities as
for solving linear equations: |
| -
simplify both sides, |
| -
bring all the terms with the variable on one side and the
constants
on the other side, |
| - and then multiply/divide both sides by the
coefficient of the variable to get the solution while applying following properties: |
|
| Properties of
inequalities |
| 1. Adding
or subtracting the same quantity from both sides of an
inequality will not change the direction of the inequality sign. |
| 2. Multiplying
or dividing both sides of an inequality by a positive number leaves the
inequality symbol unchanged. |
| 3.
Multiplying or dividing both sides of an inequality
by the same negative number, the sense of the inequality changes,
i.e., it reverses the direction of the inequality sign. |
|
| Examples
of solving single linear inequalities |
| Solve
each of the following inequalities, sketch the solution on the
real number line and express the solution in interval notation. |
|
Example:
3(x -
2) >
-2(1-
x)
|
|
Solution:
3x -
6
>
-2
+
2x |
|
x > 4 |
|
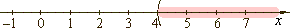 |
|
interval
notation
(4, oo) |
|
|
| The
open interval (4,
oo) contains all real numbers between given endpoints, where round
parentheses indicate exclusion of endpoints. |
|
| Example:
|
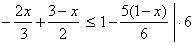 |
|
Solution: -4x
+
9 -
3x
<
6 - 5
+
5x |
|
-12x
< -8 |
|
x
> 2/3 |
|
|
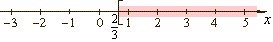 |
| interval
notation |
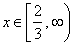 |
|
|
| The
half-closed (or half-open) interval
contains all real numbers between given endpoints, where the
square bracket indicates inclusion of the endpoint 2/3 and round
parenthesis indicates exclusion of infinity. |
|
|
Example:
(x
- 3)
· (x
+ 2)
> 0
|
| Solution:
The factor
x
- 3
has the zero at x
= 3, is negative for x
< 3
and is positive for x
> 3,
and |
|
the factor
x
+ 2
has the zero at x
= -2,
is negative for x
< - 2
and is positive for x
> -2, |
| as
is shown in the table |
| x |
-
oo |
increases |
-2 |
increases |
3 |
increases |
+
oo |
| x
+ 2 |
|
- |
0 |
+ |
+ |
+ |
|
| x
- 3 |
|
- |
- |
- |
0 |
+ |
|
| (x
- 3)(x
+ 2) |
|
+ |
0 |
- |
0 |
+ |
|
|
|
| Thus,
the given inequality is satisfied for -
oo
< x
<
- 2
or 3
<
x
< +
oo |
|
in the interval notation (
- oo
, -2
]
U [
3, +
oo
) |
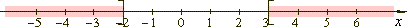 |
|
| Solving
compound or double inequalities |
| Use the same procedure to solve a compound inequality as for solving single inequalities. |
| Example:
-4
< 2(x
- 3)
< 5 |
|
|
Solution: We want the x alone as middle term and only constants in the two outer terms. Remember,
while simplifying given compound inequality, the operations that we apply to a middle term we
should also do to the both left and right side of the inequality. |
|
|
|
|
|
|
|
| Example: |
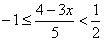 |
|
|
Solution: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Functions
contents A
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |