|
|
| Polynomial and/or Polynomial
Functions and Equations |
 Transition of the polynomial
expression from the general to source form and vice versa
Transition of the polynomial
expression from the general to source form and vice versa |
|
Deriving
the coordinates of translations formulas and the coefficients of
the source function |
|
Quadratic
function |
|
Cubic
function |
|
Quartic |
|
|
|
|
|
|
| Transition of the polynomial
expression from the general to source form and vice versa |
| Deriving
the coordinates of
translations formulas and the coefficients of the source function |
| Quadratic
function f
(x)
=
a2x2
+ a1x
+ a0 |
| 1)
Let calculate the
coordinates of translations of quadratic function using the
formulas, |
| substitute
n
= 2 in |
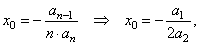 |
|
|
| then |
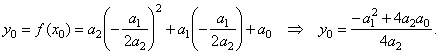 |
|
|
| 2)
To
get the source quadratic function we should plug the coordinates
of translations (with changed signs)
into the general form
of the quadratic,
i.e., |
 |
| after
expanding and reducing obtained is |
|
y
=
a2x2
the source quadratic function |
| 3)
Inversely, by plugging the coordinates of translations into the source quadratic function |
|
y
-
y0
= a2
(x
-
x0)2, |
|
|
| and
after
expanding and reducing we obtain |
|
y
=
a2x2
+ a1x
+ a0 the quadratic function
in the general form. |
|
| Cubic
function f
(x)
= a3x3
+
a2x2
+ a1x
+ a0 |
| Applying
the same method we can examine the third degree polynomial
called cubic function. |
| 1)
Calculate the
coordinates of translations |
| substitute
n
= 3
in |
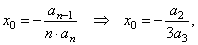 |
|
|
| then |
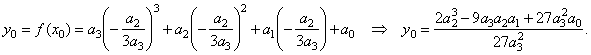 |
|
| 2)
To
get the source cubic function we should plug the coordinates
of translations (with changed signs)
into the general form
of the cubic,
i.e., |
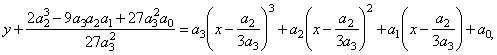 |
| after
expanding and reducing obtained is |
| |
 |
the source
cubic function. |
|
| 3)
Inversely, by plugging the coordinates of translations into the source
cubic |
|
y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0), |
|
|
|
after
expanding and reducing we obtain |
|
y
=
a3x3
+ a2x2
+ a1x
+ a0 the cubic function
in the general form. |
|
| Quartic
function y
=
a4x4
+ a3x3
+
a2x2
+
a1x + a0 |
| 1)
Calculate the
coordinates of translations by plugging
n
= 4
into |
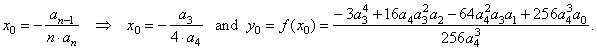
|
| 2)
To
get the source quartic function we should plug the coordinates
of translations (with changed signs) into the general form
of the quartic,
i.e., |
| y
+ y0
= a4(x
+ x0)4
+
a3(x
+ x0)3
+
a2(x
+ x0)2
+
a1(x
+ x0) +
a0, |
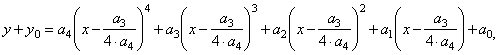 |
| after
expanding and reducing obtained is the source
quartic function |
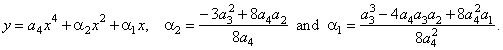
|
| 3)
Inversely, by plugging the coordinates of translations into the source
quartic |
|
y
-
y0
=
a4(x
-
x0)4
+
a2(x
-
x0)2
+
a1(x
-
x0), |
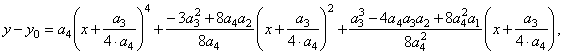
|
|
after
expanding and reducing we obtain |
|
y
= a4x4
+ a3x3
+
a2x2
+
a1x + a0
the
quartic function
in the general form. |
| Thus,
y
= a4x4
+ a3x3
+
a2x2
+
a1x + a0
or y
-
y0
=
a4(x
-
x0)4
+
a2(x
-
x0)2
+
a1(x
-
x0), |
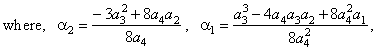 |
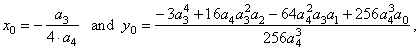 |
| by
setting x0
=
0 and y0
= 0 we get
the source quartic y
=
a4x4
+
a2x2
+
a1x. |
|
|
| According
to mathematical induction we can treat any n-degree
polynomial function using shown method. |
|
|
|
|
|
|
|
|
|
|
|
| Functions
contents C |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |