|
Infinite limits |
|
The
limit of a function examples |
|
Vertical, horizontal
and slant (or oblique) asymptotes |
|
|
|
|
|
|
| Infinite limits |
| We
write |
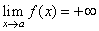 |
| if
f (x) can
be made arbitrarily large by choosing x
sufficiently close
but not equal to a. |
| We
write |
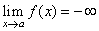 |
| if
f (x) can
be made arbitrarily large negative by choosing x
sufficiently close
but not equal to a. |
|
| The
limit of a function examples |
| Example: Evaluate
the following limits; |
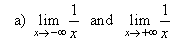 |
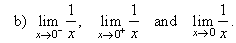 |
| Solution:
a) As x
tends to minus infinity f
(x) |
|
gets closer and closer to 0. |
| As x
tends to plus infinity f
(x)
gets closer and |
|
closer to 0. Therefore, |
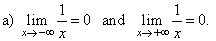 |
| b)
As x
tends to 0 from the left f
(x)
gets larger in |
| negative sense. |
|
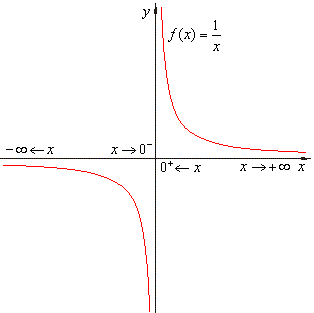 |
|
| As
x
tends to 0 from the right f(x)
gets larger in positive sense. Therefore, |
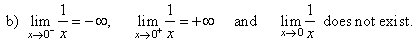 |
|
| Vertical, horizontal
and slant (or oblique) asymptotes |
| If
a point (x, y) moves
along a curve f
(x)
and then at least one of its coordinates tends to infinity,
while the distance between the point and a line tends to zero
then, the line is called the asymptote
of the curve. |
|
| Vertical
asymptote |
| If
there exists a number a
such that |
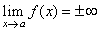 |
| then
the line x
= a is the vertical
asymptote. |
|
| Horizontal
asymptote |
| If
there exists a number c
such that |
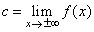 |
| then
the line y
= c is the horizontal
asymptote. |
|
| Slant
or oblique asymptote |
| If
there exist limits |
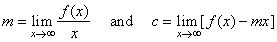 |
| then,
a line y = mx
+ c is the slant
asymptote of the function f
(x). |
|
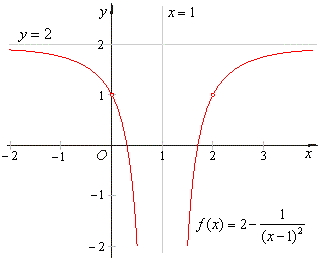
| Example: Find
the vertical and the horizontal |
| asymptote
of the function |
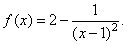 |
| Solution:
Since, |
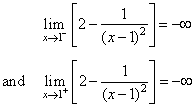 |
| then x
= 1 is the vertical asymptote. |
|
 |
|
| Since, |
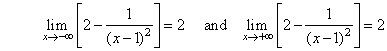 |
|
|
| then y
= 2 is the horizontal asymptote. |
|