|
The
limit of a function examples |
|
Monotone
functions - increasing or decreasing in value |
|
|
|
|
|
|
| The
limit of a function examples |
| Example: Find
the vertical and the horizontal |
| asymptote
of the function |
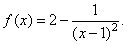 |
| Solution:
Since, |
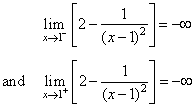 |
| then x
= 1 is the vertical asymptote. |
|
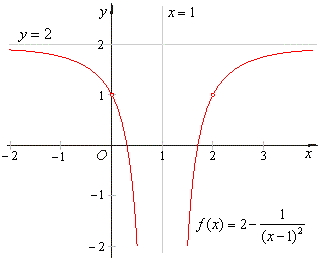 |
|
| Since, |
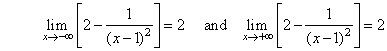 |
|
|
| then y
= 2 is the horizontal asymptote. |
|
| Example: Calculate
asymptotes and sketch the graph of the function |
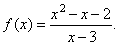 |
|
| Solution:
By
equating the numerator with zero and |
| solving for
x
we
find the x-intercepts, |
| x2
-
x -
2 = (x + 1)(x -
2) = 0, |
| x1
= -1
and
x2
= 2. |
| We
calculate f(0)
to find the y-intercept, |
| f(0)
= 2/3. |
| By
equating the denominator with zero and solving |
| for
x
we find the vertical
asymptote, |
| x
= 3. |
| Let
calculate following limits |
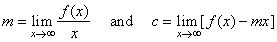 |
| to
find the slant asymptote y
= mx + c. |
|
 |
|
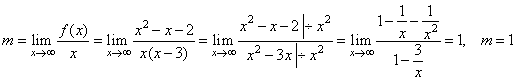 |
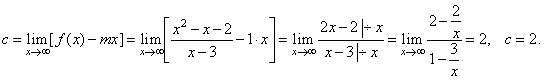 |
| Therefore,
the line y
= x + 2
is the slant asymptote of the given function. |
|
| Example: Find
the following limits, |
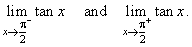 |
| Solution:
The graph of the tangent
function shows, |
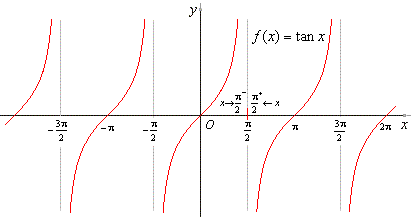 |
| as
x
approaches
p/2 from the left,
the tangent
function increases
to plus infinity, while as x
approaches
p/2
from the
right, the function decreases to minus infinity, therefore |
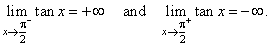 |
|
| Example: Evaluate
the limit |
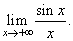 |
|
| Solution:
|
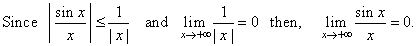 |
|
|
| Example: Evaluate
the limits, |
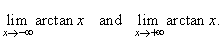 |
|
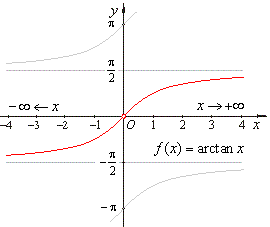
| Solution:
The graph of the
arc-tangent
function |
| shows,
as x
tends to minus infinity the function |
| values
approach -
p/2
while, as x
tends to plus |
| infinity,
the function values approach p/2. |
| Therefore, |
 |
| and |
 |
|
 |
|
|
| Monotone
functions - increasing or decreasing in value |
| 1.
The function is said to be increasing if f
(x1)
< f (x2)
for all x1
<
x2. |
| 2.
The function is said to be decreasing if f
(x1)
> f (x2)
for all x1
<
x2. |
| 3.
If f
is either increasing or decreasing then f
is said to be monotone. |