|
| Integral
calculus |
|
|
|
The
indefinite integral |
Integration by parts rule |
|
The indefinite integrals
containing quadratic polynomial (trinomial)
|
|
The indefinite integrals
containing quadratic polynomial, examples
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Integration
by parts rule
|
|
The rule for differentiating the
product of two differentiable functions leads to the integration
by parts formula.
|
|
Let f
(x)
and g
(x)
are differentiable functions, then the product rule gives
|
|
[ f
(x) g (x)]'
= f (x)
g (x)' + g (x)
f ' (x),
|
| by
integrating both sides |
|
|
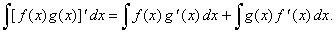
Since the integral of the derivative
of a function is the function itself, then
|
|
|
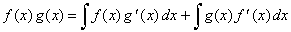
and by rearranging obtained is
|
|
|
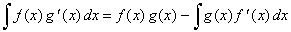
the integration by parts
formula.
|
|
By substituting
u = f
(x) and
v
= g (x)
then, du =
f ' (x)
dx and dv
= g' (x)
dx, so that
|
|
|
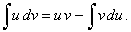
To apply the above formula, the
integrand of a given integral should represent the product of one
function and the differential of the other.
|
|
The selection of the function
u and the differential dv
should simplify the
evaluation of the remaining integral.
|
|
In some cases it will be necessary to
apply the integration by parts repeatedly to obtain a simpler
integral.
|
|
|
|
The indefinite integrals
containing quadratic polynomial (trinomial)
|
| Recall
that the quadratic polynomial y
= ax2 + bx + c
represents the expansion of the translatable form of
its source function y
= ax2 in the direction of the coordinate axes, thus
|
|
|
|
|
|
|
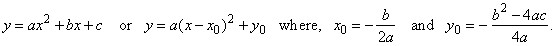
We solve given integral by separating
the derivative of the quadratic polynomial in the numerator, thus
|
|
|
|
therefore, the solution of I2
depend on the leading coefficient a
and the vertical translation y0,
i.e.,
|
| a
)
if |
 |
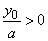then, |
|
|
|
|
| b
) if |
 |
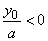then, |
|
|
|
|
|
c
) if
y0 = 0
then,
|
|
|
|
|
|
|
|
|
|
The integrand function to be real, the
quadratic polynomial in the denominator must be positive,
therefore
|
|
a
) if a
> 0 and
y0
is not
0 then
|
|
|
|
b
) if a
< 0 and
y0
>
0 then
|
|
|
|
c
) if a
> 0 and
y0 =
0 then
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Functions
contents G |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
