|
|
|
Exponential and Logarithmic
Functions and Equations
|
 Inverse functions
Inverse functions |
 Exponential functions
Exponential functions
|
|
Translated logarithmic
and exponential functions |
|
|
|
|
|
|
|
Exponential and
logarithmic functions
|
| Exponential
and logarithmic functions are mutually inverse functions |
|
| Inverse functions |
| The inverse function, usually written
f -1, is the function whose
domain and the range are respectively the range and domain of a given function
f, that is |
| f
-1(x)
= y if and only if
ƒ (y)
= x . |
| Thus, the
composition of the inverse function and the given function returns
x, which is called the
identity function, i.e., |
| f
-1(ƒ (x))
= x and
ƒ (f
-1
(x))
= x. |
| The inverse of a function undoes the procedure
(or function) of the given function. |
| A pair of inverse functions is in
inverse relation. |
| Example: If
given
ƒ(x)
= log2 x
then f -1(x)
= 2x
since, |
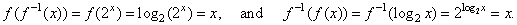 |
|
| Therefore,
to obtain the inverse of a function y = ƒ
(x), exchange the variables
x
and y,
i.e., write x = ƒ (y)
and solve for y.
Or form the composition ƒ (f
-1(x))
= x and solve
for f -1. |
|
| Example: Given
y = ƒ (x)
= log2 x determine
f -1(x). |
| Solution:
a) Rewrite
y = ƒ (x)
= log2 x
to x =
log2 y
and solve for y,
which gives y =
f
-1(x)
= 2x. |
|
b) Form ƒ (f
-1(x))
= x that
is, log2
(f -1(x))
= x and
solve for f -1, which
gives f -1(x)
= 2x. |
|
| The
graphs of a pair of inverse functions are symmetrical with
respect to the line
y
= x. |
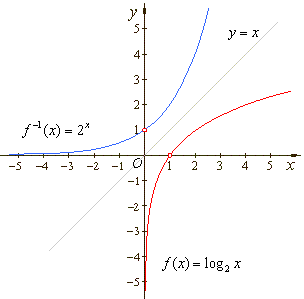 |
|
| Exponential functions
|
|
- Exponential
function |
y
= ex
<=>
x = ln y,
e = 2.718281828...the
base of the natural logarithm. |
|
|
The exponential
function is inverse
of the natural logarithm
function, so that eln
x = x. |
|
- Exponential
function |
y =
ax
<=>
x = loga
y,
where a > 0 and
a is not
1. |
|
|
The exponential
function with base a
is
inverse of the logarithmic
function, so that |
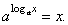 |
|
|
| The
graph of the exponential
function y
= ax = ebx,
a
> 0
and b
= ln a |
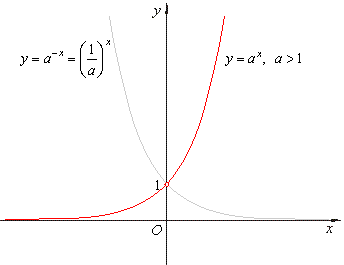 |
| The
exponential
function is
inverse of the logarithmic
function since its
domain and the range are respectively the range and domain of
the
logarithmic
function, so that |
| ƒ
(f
-1(x))
= x that
is, ƒ
(f
-1(x))
= ƒ (ax)
= loga (ax) =
x. |
| The
domain of ƒ
(x)
= ax is the set of all real
numbers. |
| The
range of the ƒ
(x)
= ax is the set of all positive
real numbers. |
| If
a > 1 then
ƒ
is an increasing function and if
0
< a < 1 then ƒ
is a decreasing function. |
| The
graph of the exponential
function passes through the point (0,
1). The x-axis
is the horizontal asymptote to the graph, as shows the above
picture. |
|
| Translated logarithmic
and exponential functions |
| Example: Given
translated logarithmic function y -
2 = log3 (x + 1), find
its inverse and draw their
graphs. |
| Solution:
Exchange the variables
and solve for y,
that is x -
2 = log3 (y + 1)
which gives y
+ 1 = 3x
-
2. |
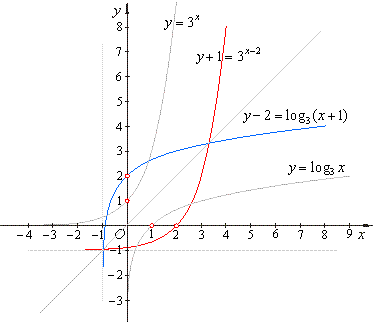 |
| Note
that y -
y0
= loga (x
-
x0)
represents translated
logarithmic function to base a |
|
and y -
y0 =
a
(x
-
x0)
represents translated
exponential function with base a |
|
where, x0
and y0
are the coordinates of translations of the graph in the
direction of the coordinate axes. |
|
|
|
|
|
|