|
|
Applications of the derivative |
 Differential
of a function
Differential
of a function |
|
Use
of differential to approximate the value of a function |
|
Rules
for differentials |
|
Differentials of some
basic functions |
|
|
|
|
|
|
|
| Differential
of a function |
| If
given y = f (x)
is differentiable function then, the derivative of y
or f (x) |
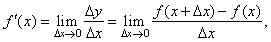 |
| as
the instantaneous rate of change of y
with respect to x,
can also be written as |
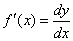 |
| where, the increment
Dx
= dx is called differential of
the independent variable and dy
is the differential of y. |
| Therefore,
the differential of a function |
| dy
= f '(x)dx |
| represent
the main part of the increment Dy
which is linear concerning the increment Dx
= dx, as is shown |
| in
the figure below. |
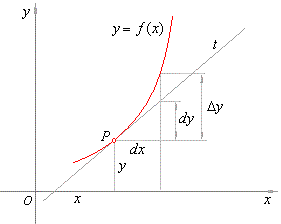 |
|
|
Example:
Find
the increment Dy
and the differential dy
of the
function f
(x)
= x2 -
4x,
and
calculate their values
if x
= 3
and Dx
= 0.01.
|
|
Solution:
Since
Dy
= f (x + Dx)
-
f
(x)
then
Dy
= (x + Dx)2
-
4(x
+ Dx)
-
(x2 -
4x)
|
| Dy
= (2x
-
4)Dx
+ Dx2
therefore,
dy
= (2x
-
4)Dx
= (2x
-
4)dx |
|
or
f '(x)
= 2x
-
4,
dy
= f '(x)dx
= (2x
-
4)dx. |
| Let
calculate the values of Dy
and dy
for
x
= 3
and Dx
= 0.01, |
|
Dy
= (2x
-
4)Dx
+ Dx2
= (2
·
3
-
4)
·
0.01
+ 0.012
= 0.0201, |
|
and dy
= f '(x)Dx,
dy
= (2x
-
4)Dx
= (2
·
3
-
4)
·
0.01
= 0.02. |
|
| Use
of differential to approximate the value of a function |
| If
the change of the independent variable (increment)
Dx
is
small then, the differential dy
of a function y = f
(x) and
the increment
Dy
are approximately equal, |
|
Dy
»
dy
that is, f
(x + Dx)
-
f(x)
= f '(x)Dx
|
|
or
f
(x + Dx)
»
f(x)
+ f '(x)Dx. |
|
|
Example:
Using
the differential calculate approximate value of cos
61°.
|
|
Solution:
Since
we must use radians as units of measurement of angles, let first
convert degrees to radians.
|
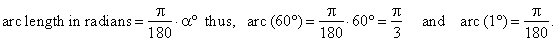 |
| Using
the formula |
| f
(x + Dx)
»
f
(x)
+ f '(x)Dx
and
taking,
f
(x)
= cos
x
where,
x =
arc (60°)
and Dx
= arc (1°) |
|
therefore, |
| cos
(x + Dx)
» cos
x
+ (cos
x)'
· Dx
where,
x =
p/3
and
Dx =
p/180 |
|
or cos
61°
» cos
(p/3)
+ (
-
sin
(p/3))
· (p/180) =
1/2
-
(Ö3
/2)
· 0.0174,
cos
61°
» 0.4849. |
|
|
Example:
Using
the differential calculate approximate value of e
0.15.
|
|
Solution:
Using
the formula
|
| f
(x
+ Dx)
»
f
(x)
+ f '(x)Dx
and
taking,
f
(x)
= ex
where,
x
= 0
and Dx
= 0.15 |
|
then, ex
+ Dx
»
ex
+ (ex)'
· Dx
that
is,
e 0.15
»
e
0
+ e
0
· 0.15
= 1 + 0.15
= 1.15. |
|
|
Example:
Approximately,
how much will increase the volume of the sphere if its
radius r
= 20
cm increases
by 2 mm.
|
|
|
Solution:
Using
approximation Dy
»
dy
or Dy
= f (x + Dx)
-
f
(x)
»
f '(x)Dx
|
|
therefore, DV
»
V '(r)Dr. |
| Since
V
= (4/3)pr3
then V '(r)
= (4/3)p
· 3r2
= 4pr2, |
| and
by substituting r
= 20
and Dr
= 0.2
into |
| DV
»
V '(r)Dr
= 4pr2
· Dx
we get
DV
»
4p
· 202
· 0.2
= 1005,3
cm3. |
|
| Rules
for differentials |
| Rules
for differentials are the same to those for derivatives, such that |
|
1) dc = 0,
c
is a constant |
|
2) dx = Dx,
x
is the independent variable |
|
3) d(cu) = c
du |
|
4)
d(u ±
v) = du ±
dv |
|
5) d(u v) = u
dv ±
v du |
| 6) |
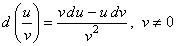 |
|
|
7) d
f(u) = f ' (u) du. |
|
|
Differentials
of some basic functions |
|
1) d
un = n
un -
1du |
|
2) d
eu = eu
du |
|
3)
d
an = an ln a
du |
| 4) |
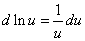 |
|
|
5) d
sin u = cos u
du |
|
6) d
cos u = -
sin u
du |
| 7) |
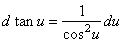 |
|
| 8) |
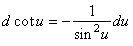 |
|
| 9) |
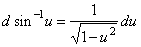 |
|
| 10) |
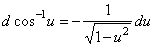 |
|
| 11) |
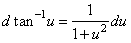 |
|
| 12) |
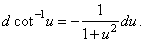 |
|
|
|
Example:
To
show the use of the formula 2) d
eu = eu du
above, let substitute;
a) u =
x,
b) u = cos
x
|
| and
c) u = x3. |
|
Solution:
a)
By substituting u =
x,
obtained is d
ex = ex dx
|
|
b) By substituting u =
cos x,
we get d
e cos x = ecos x
d (cos x) =
-
e cos x sin x
dx |
| |
c)
By substituting u =
x3,
we get |
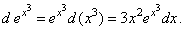 |
|