|
|
Applications of the derivative |
 Angle
between two curves
Angle
between two curves |
|
Angle
between two curves, examples |
|
|
|
|
|
|
|
| Angle
between two curves |
| Angle between two curves is the angle subtended by tangent lines at the point where the curves
intersect. |
| If curves
f1(x)
and f2(x)
intercept at P(x0,
y0)
then |
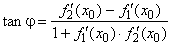 |
| as
shows the right figure. |
| |
|
 |
|
|
| Angle
between two curves examples |
| Example: Find
the angle between cubic y
= -
x3 + 6x2 -
14x + 14 and quadratic y
= -
x2 + 6x -
6 |
| polynomial. |
| Solution: To
find the point where the curves intersect we should solve their
equations as the system of two equations
in two unknowns simultaneously. Therefore, |
| -
x3 + 6x2 -
1
4x + 14
= -
x2 + 6x -
6
or x3
-
7x2 + 20x -
20 = 0
|
| the
root of the cubic equation we calculate using the formula |
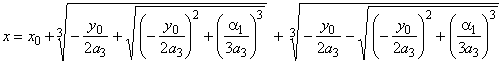 |
| where, |
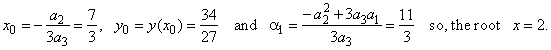 |
|
| Then, we
calculate the slopes of the tangents drown to the given cubic and the
quadratic polynomial by evaluating
their derivatives at x
= 2. Thus, |
| taking
f2(x)
= -
x3 + 6x2 -
14x + 14
so that f
'2(x)
= -
3x2 + 12x -
14
then f '2(2)
= -
2 |
|
and f1(x)
= -
x2 + 6x -
6
so that f '1(x)
= -
2x + 6
then f '1(2)
= 2. |
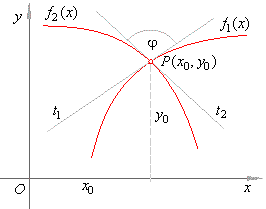
| Finally
we plug the slopes of tangents into the formula to find the angle
between given curves, as shows the |
|
figure below. |
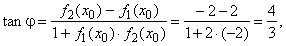 |
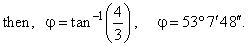 |
| We
sketch the graphs of the quadratic and the |
| cubic
by calculating coordinates of translations x0 |
| and
y0,
as they are at the same time the |
| coordinates
of the maximum and the point of |
| inflection
respectively, thus |
| (x0)2
= xmax
= -
a1/(2a2) = 3,
y0
= f1(x0)
= 3, |
| (x0)3
= xinfl
= -
a2/(3a3) = 2,
y0
= f2(x0)
= 2. |
|
 |
|
|
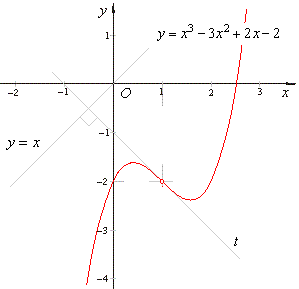
| Example: At
which point of the cubic y
= x3
-
3x2 + 2x -
2 is its tangent perpendicular to the
line y
= x. |
| Solution: Since
the slopes of perpendicular lines are negative reciprocals of each other
then, the slope of |
| the
tangent to the cubic has to be
f ' (x)
= -1
to be perpendicular to the given line whose slope m
= 1. |
| Therefore, |
| f '
(x)
= 3x2 -
6x + 2,
we set f '
(x)
= -1
or 3x2
-
6x + 2
= -1
that gives x
= 1 |
|
the abscissa of the tangency point. Then, plug x
= 1 into the given cubic to calculate
its ordinate, |
| y
= x3
-
3x2 + 2x -
2,
y (1)
= -
2
so the tangency point I
(1,
-2). |
| We
sketch the graph of the cubic
by calculating |
| coordinates of translations
x0
and
y0, |
| x0
= xinfl
= -
a2/(3a3) = 1,
y0
= f (x0)
= - 2 |
| what
coincide with the coordinates
of the point of |
| inflection
I (1,
-2). |
| By
plugging x0
and
y0,
with changed signs, into the |
| given
cubic, |
| y
- 2
= (x + 1)3
-
3(x +
1)2 + 2(x +
1) -
2 |
| we
get its source form |
| fs
(x)
= x3 -
x
or fs
(x)
= a3x3
+ a1x |
|
 |
|
| where
a1
= -
(a2)2 /(3a3)
+ a1,
a1
=
-1
and a1
= tan at,
as shows the figure above. |
|