|
| Conic
Sections |
|
|
|
Hyperbola
and Line
|
 Hyperbola and line relationships
|
|
Condition for a line to be the tangent to the hyperbola -
tangency condition |
|
The equation of the tangent at the point on the hyperbola
|
|
Polar and pole of the hyperbola
|
|
Construction of the tangent at the point on the hyperbola
|
|
Construction of tangents from a point outside the hyperbola
|
|
Hyperbola and
line examples
|
|
|
|
|
|
|
| Hyperbola and line relationships
|
| Let examine relationships between a hyperbola and a line passing through the center of the hyperbola, i.e., the
origin. A line y =
mx intersects the hyperbola at two
points if
|
|
the slope |m|
<
b/a but
if |m|
> b/a
then,
|
|
the line y =
mx does not intersect the hyperbola at all.
|
| The diameters of a hyperbola are straight lines
passing through its center.
|
|
The asymptotes divide these two pencils of diameters
into, one which intersects the curve at two points, and
the
other which do not intersect.
|
A diameter of a conic section is a line which passes
through the midpoints of parallel chords.
|
Conjugate diameters of the hyperbola (or the ellipse)
are two diameters such that each bisects all chords
drawn parallel to the other.
|
|
 |
|
| As the equation of a hyperbola can be obtained from the equation of an ellipse by changing the sign of
b2
|
|
that is, a2(1
-
e2)
= -a2(e2
-
1) =
-b2, |
| this way, we can use other formulas relating to the ellipse to obtain corresponding
formulas for the hyperbola. |
| Therefore, when we examine conditions which determine position of a line in relation to a hyperbola that is, |
| when
solve the system of
equations,
y =
mx + c |
| b2x2
-
a2y2
= a2b2
|
| |
|
then if, a2m2
-
b2
> c2
the line intersects the hyperbola at two points,
|
|
a2m2
-
b2 = c2
the line is the tangent of the hyperbola,
|
|
a2m2
-
b2
< c2
the line and the hyperbola do not intersect. |
|
| Condition for a line to be the tangent to the hyperbola -
tangency condition
|
| A line is the tangent to the hyperbola if
|
a2m2
-
b2 = c2. |
|
|
| Regarding
the asymptotes, to which c
= 0, this condition gives
|m|
= b/a
and that is why we can say that the hyperbola touches the asymptotes at infinity. |
| From the tangency condition it also follows that the slopes of the tangents
will satisfy the condition if |
|
|
| That is, the tangents to the hyperbola can only be parallel to a line belonging to the pencil of lines that do not
intersect the hyperbola. |
|
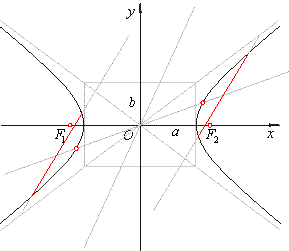
| The equation of the tangent at the point on the hyperbola
|
As we already mentioned, the points of contact of a line and the hyperbola can be obtained from the
corresponding formula for the ellipse by changing b2
with -b2
thus |
|
 |
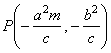the
tangency point or the point of contact. |
|
| So, the intercept and slope of the
tangent |
 |
|
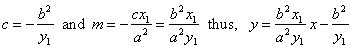| or |
b2x1x
-
a2y1y
= a2b2 |
the equation of the tangent at a point
P1(x1,
y1)
on the hyperbola.
|
|
|
| Polar and pole of the hyperbola
|
If from a point
A(x0, y0), exterior to the hyperbola, drawn are tangents, then the secant line passing through
the contact points, is the polar of the point A.
The point A
is called the pole of the polar. |
| The equation of the
polar is derived the same way as for the ellipse, |
| |
b2x0x
-
a2y0y
= a2b2 |
the equation of the
polar of the point A(x0, y0). |
|
|
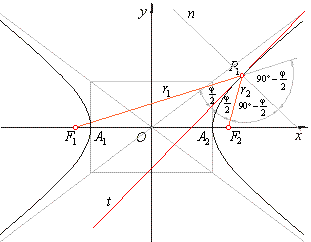
| Construction of the tangent at the point on the hyperbola
|
| The tangent at the point
P1(x1,
y1)
on the hyperbola is the bisector of the angle F1P1F2
subtended by focal |
|
radii,
r1
and
r2 at
P1 .
|
|
The proof shown for the ellipse applied to
the hyperbola gives,
|
|
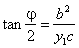
| or |
 |
|
|
|
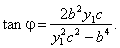See the title
'
The angle between the focal radii at a point of the
ellipse'.
|
|
 |
|
|
|
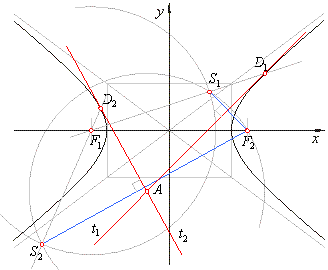
| Construction of tangents from a point outside the hyperbola |
|
With A as center draw an arc through
F2,
and from F1as center, draw an arc of radius
2a.
|
|
These arcs intersect at points
S1
and
S2.
|
|
Tangents are the
perpendicular bisectors of the line segments F2S1
and
F2S2.
|
|
Tangents can also be drawn as lines through
A and
the intersection points of lines through F1S1
and
F1S2,
with the hyperbola.
|
|
These intersections are at the same
time the points of contact
D1
and
D2.
|
|
 |
|
|
|
| Hyperbola and line examples
|
| Example:
Determine the
semi-axis
a
such that the line
5x
-
4y
-
16 = 0 be the tangent of the hyperbola |
| 9x2
-
a2y2 = 9a2. |
|
Solution:
Rewrite the equation
9x2
-
a2y2 = 9a2 | ¸
9a2
|
|
|
| and
the equation of the tangent 5x
-
4y
-
16 = 0
or |
 |
|
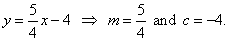| Then,
plug the slope and the intercept into tangency condition,
|
 |
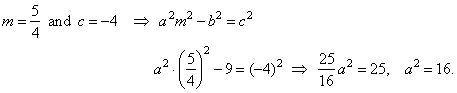| Therefore,
the given line is the tangent of the hyperbola |
 |
|
|
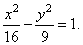| Example:
Find the angle
between the ellipse, which passes through points, A(Ö5,
4/3) and B(1,
4Ö2/3), and
the hyperbola whose asymptotes are y
= ±
x/ 2
and the linear eccentricity or half of the focal distance |
| c
= Ö5. |
|
Solution:
Find
the equation of the ellipse by solving the system of
equations, |
|
|
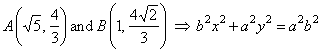
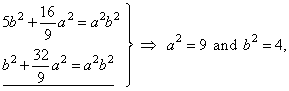
| thus,
the equation of the ellipse |
 |
|
|
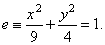The equation of the hyperbola by solving the system of
equations,
|
|
 |
|
 |
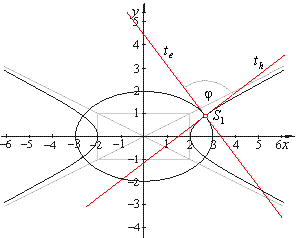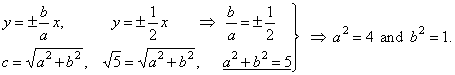| Therefore, equation of the hyperbola |
 |
|
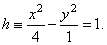| Angle between curves is the angle between tangents at intersection of the curves. By solving the system of
equations of the curves we obtain the points of intersection, |
| (1)
4x2
+ 9y2 = 36 (2)
=> (1)
4(4y2
+ 4) + 9y2 = 36,
25y2 = 20,
y1,2 = ±2/Ö5,
x1,2 = ±6/Ö5 |
|
(2) x2
-
4y2 = 4
=>
x2 = 4y2
+ 4 |
| Tangent
of the ellipse and the hyperbola at the intersection S1(6/Ö5,
2/Ö5), |
|
S1(6/Ö5,
2/Ö5)
=> te
::
b2x1x
+ a2y1y
= a2b2,
4x + 3y
= 6/Ö5
or y =
(-4/3)x
+ 2Ö5, |
|
S1(6/Ö5,
2/Ö5)
=>
th
::
b2x1x
-
a2y1y
= a2b2,
3x -
4y = 2/Ö5
or y
= (3/4)x -
Ö5/2. |
 |
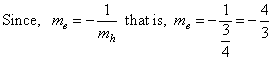| fulfilled is the perpendicularity condition.
Therefore, the angle between curves j
= 90°. |
|
|
|
|
|
|
|
|
|
|
| Conic
sections contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
