|
| Conic
Sections |
|
|
|
Hyperbola
|
|
Examples of hyperbola |
Equilateral or rectangular hyperbola with the coordinate axes as its
asymptote
|
|
Translation
of equilateral or rectangular hyperbola with the coordinate axes as its
asymptote |
|
|
|
|
|
|
| Examples
of hyperbola |
Example:
Given is the hyperbola
4x2 -
9y2 = 36,
determine the semi-axes, equations of the asymptotes,
coordinates of foci, the eccentricity and the semi-latus rectum.
|
Solution:
Put the equation in the standard form to
determine the semi-axes, thus
|
|
4x2
-
9y2 = 36 | ¸
36
|
|
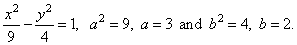
| Asymptotes, |
 |
|
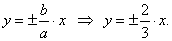| Applying, |
 |
|
|
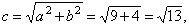coordinates of foci, F1(-Ö13,
0) and
F2(Ö13,
0).
|
|
 |
|
| The eccentricity, |
 |
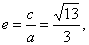and the
semi-latus rectum,
|
 |
|
|
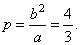| Example:
Write equation of a hyperbola with the focus at
F2(5,
0) and whose asymptotes are, |
 |
|
|
|
 |
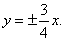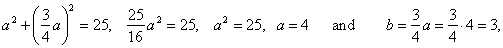| Therefore,
the equation of the hyperbola,
|
 |
|
|
|
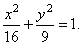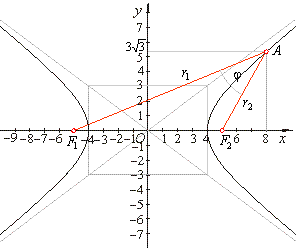
| Example:
Find the angle subtended by the focal radii
r1
and
r2
at a point A(8, y
> 0) of the hyperbola
|
| 9x2
-
16y2 = 144. |
|
Solution:
We determine the ordinate of the point
A
by plugging its abscissa into equation of the hyperbola,
|
|
x
= 8 =>
9x2
-
16y2 = 144
|
|
9 · 82
-
16y2 = 144,
|
|
16y2 = 432 =>
y2 =
27,
|
|
y1,2 = ±3Ö3
so that A(8,
3Ö3).
|
|
The equations of the lines of the radii r1
and
r2, we
write
using the formula of a line through two
points. Since,
|
| r1::
AF1 and
F1(-c,
0) ,
and |
 |
|
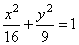| then |
 |
|
|
 |
|
 |
 |
|
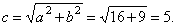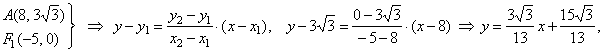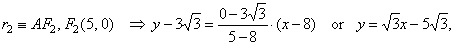Therefore, the angle between the focal radii r1
and
r2
at the point A
of the hyperbola, as
|
 |
|
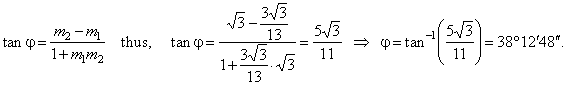| Example:
The hyperbola is given by equation
4x2
-
9y2 + 32x + 54y -
53 =
0. |
| Find coordinates of the
center, the foci, the eccentricity and the asymptotes of the hyperbola. |
| Solution:
The given hyperbola is translated in the direction of the coordinate axes so the values of
translations x0 and
y0
we can find by using the method of completing the square
rewriting the equation in |
| the standard
form, |
 |
|
|
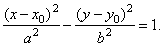Thus,
4x2 + 32x
-
9y2 + 54y -
53 =
0,
|
|
4(x2 + 8x) -
9(y2 -
6y) -
53 =
0
|
|
4[(x +
4)2 -
16] -
9[(y -
3)2 -
9] -
53 =
0
|
|
4(x + 4)2 -
9(y -
3)2 = 36 | ¸
36
|
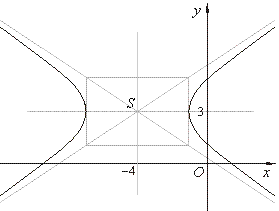
| Therefore,
|
 |
|
|
 |
|
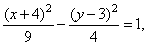| it
follows that a2 =
9, a
= 3,
b2 = 4,
b
= 2,
and the center of the hyperbola at S(x0, y0)
or S(-4,
3). |
| Half
the focal distance |
 |
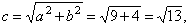the
eccentricity |
 |
|
|
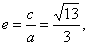and the foci, F1(x0
-
c,
0) so
F1(-4
-
Ö13,
0) and
F2(x0
+ c,
0),
F1(-4
+ Ö13,
0). |
| Equations of the asymptotes of a translated hyperbola |
 |
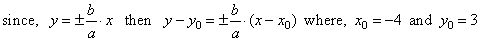| therefore, the asymptotes of the given
hyperbola, |
 |
|
|
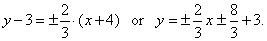| Example:
Write the equation of the hyperbola 9x2
-
25y2 = 225
in the vertex form. |
| Solution:
Using parallel shifting we should place the center of the hyperbola at
S(-a,
0). |
| Rewrite
9x2
-
25y2 = 225 | ¸
225 |
|
 |
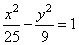therefore,
a = 5 and
b = 3,
so that S(-5,
0). |
|
|
Then, the translated
hyperbola with the center at S(-5,
0) has the equation
|
 |
|
| Equilateral or rectangular hyperbola with the coordinate axes as its
asymptote
|
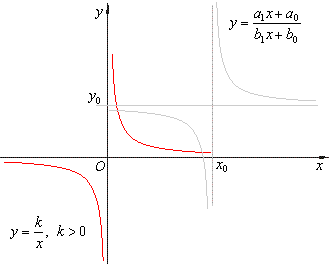
| The
graph of the reciprocal function y
= 1/x or y
= k/x is a rectangular
(or right) hyperbola of which asymptotes are the coordinate axes. |
| If k
> 0 then, the
function is decreasing from zero to negative infinity
and from positive infinity to zero, i.e., the graph of
the rectangular hyperbola opening in the first and third
quadrants as is shown in the right figure. |
| The vertices, |
 |
|
|
|
 |
|
|
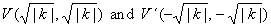| Translation
of equilateral or rectangular hyperbola with the coordinate axes as its
asymptote |
| The rational function |
 |
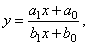by dividing the
numerator by denominator, |
|
| can be
rewritten into |
 |
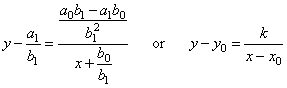where, |
 |
|
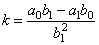| is the constant, |
 |
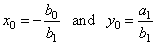are the vertical and
the horizontal asymptote respectively. |
|
| Therefore,
the values of the vertical and the horizontal asymptotes correspond to
the coordinates of the horizontal and the vertical translation of the
reciprocal function y
= k/x as is shown in
the figure below. |
 |
|
|
|
|
|
|
|
|
|
|
| Conic
sections contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
