|
|
Vectors in a Plane and Space |
|
|
 Vectors
and a coordinate system, Cartesian vectors
Vectors
and a coordinate system, Cartesian vectors |
 Vectors in
a coordinate plane (a two-dimensional system of coordinates), Cartesian
vectors
Vectors in
a coordinate plane (a two-dimensional system of coordinates), Cartesian
vectors |
|
Radius vector or position vector |
|
Vector components |
|
Vectors in
a two-dimensional system, examples |
|
|
|
|
|
|
| Vectors
and a coordinate system, Cartesian
vectors |
| Vectors in
a coordinate plane (a two-dimensional system of coordinates), Cartesian
vectors |
| By introducing a coordinate system in a plane with the unit vectors,
i and
j
(in direction of x
and y
coordinate axis, respectively) whose tails are in the origin O, then each point of the plane determines a vector
r
= OP. |
| A directed line segment from the origin to a point
P (x,
y) in plane is called a
radius vector and denoted
r. |
| The radius
(or position) vector equals the sum of its
vector components,
xi
and y j
in direction of coordinate axes, that is |
|
|
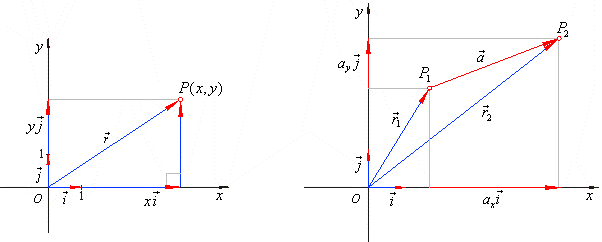 |
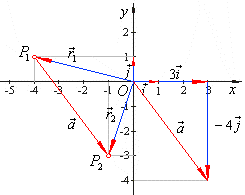
| Consider
a vector a
in the plane directed from a point
P1(x1,
y1)
to P2(x2,
y2)
shown in the right diagram, it also equals to the sum of corresponding
vector components
axi
and
ayj,
in direction of coordinate axes,
|
|
|
| The diagram shows that |
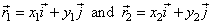 |
are the radius vectors of
points P1 and
P2, |
|
| thus
the vector a
equals to the difference (joins their heads), that is |
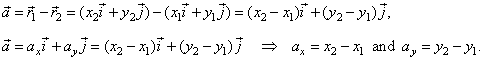 |
It is obvious from the above diagrams that a vector and its components, i.e., its projections in direction of
coordinate axes, form a right triangle, from which, according to Pythagorasí theorem, we determine the length
of the vector, |
|
|
|
| Example:
Determine a vector a whose tail is at the point
P1(-4,
1) and head at the point
P2(-1,
-3).
|
| Solution:
Points, P1 and
P2 determine radius vectors, |
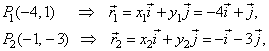 |
| therefore, |
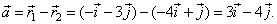 |
|
 |
|
|
| Example:
At what point P1(x1,
y1) has the vector
a
= -7i
+ 2j
its tail, if its head is at the point
|
| P2(3,
-4)? |
| Solution: |
Using |
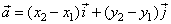 |
or after substitution |
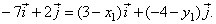 |
|
|
| Knowing that two vectors are equal if their corresponding scalar (numeric) components are equal, it follows |
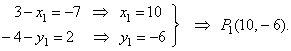 |
|
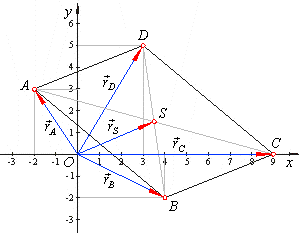
| Example:
To a parallelogram given are vertices, A(-2,
3), B(4,
-2)
and D(3,
5). Determine coordinates of the
vertex C
and the intersection point S
of the diagonals.
|
| Solution:
To the given vertices point radius vectors, |
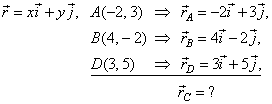 |
| According to the diagram, the radius vector of the point
C, |
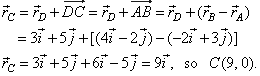 |
|
 |
|
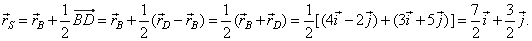
|
|
Hence, the intersection point S
of the diagonals S(7/2,
3/2).
|
|
| Example:
Given are vectors, a
= -2i
+ 3j
and b
= 4i
+ a
j, determine the coefficient
a
such that the vectors to be collinear.
|
| Solution:
In order vectors to be collinear must be |
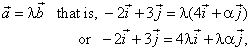 |
| as two vectors are equal if their corresponding scalar components are equal,
then |
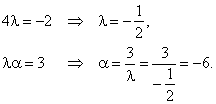 |
|
 |
|
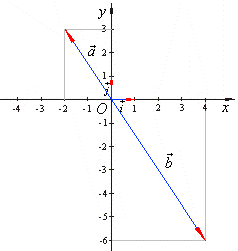
|
Vectors, a
= -2i
+ 3j
and b
= 4i -
6
j
are collinear, as shows diagram in the above figure.
|
|
|
|
|
|
|
|
|
|
|
| College
algebra contents
F |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
|
|