|
|
Vectors in a Plane and Space |
|
 Vectors in
three-dimensional space in terms of Cartesian coordinates
Vectors in
three-dimensional space in terms of Cartesian coordinates |
|
Angles of
vectors in relation to coordinate axes, directional cosines - scalar
components of a vector |
|
The unit vector of a vector |
|
Vectors in
a three-dimensional coordinate system, examples |
|
|
|
|
|
|
|
|
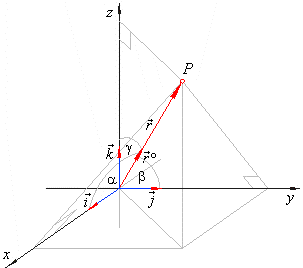
Vectors in
three-dimensional space in terms of Cartesian coordinates
|
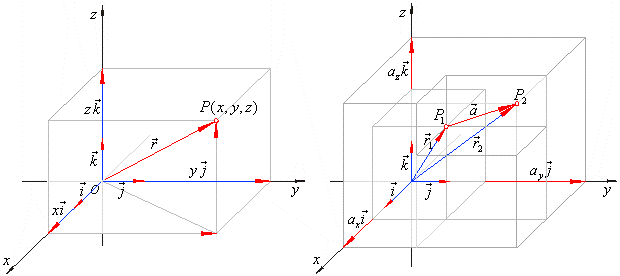
By introducing three mutually perpendicular unit
vectors, i,
j and
k, in direction of coordinate axes of the
three-dimensional coordinate system, called
standard basis vectors, every point
P (x,
y, z) of the space
determines the radius vector or the position vector,
|
|
|
|
|
Similarly, a vector a
in the right diagram, which is directed from a point P1(x1,
y1, z1)
to a point P2(x2,
y2, z2)
in space, equals to sum of its vector components, axi,
ay j,
and
azk,
in the direction of the coordinate axes,
|
|
x,
y, and
z
respectively, that is
|
|
|
| The vector
a represents the difference of the radius vectors, |
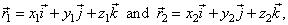 |
|
| thus |
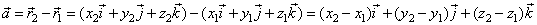 |
|
|
|
|
|
so the scalar (numeric) components of the vector
a,
|
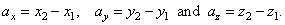
|
|
Therefore, the length of the vector
a,
|
|
|
|
|
|
Angles of vectors in relation
to coordinate axes, directional cosines - scalar components of a vector
|
|
The scalar components of a vector and its magnitude form a right triangle in which the hypotenuse equals
the magnitude of the vector, then
|
|
|
| since
b
= 90° -
a
then cosb
= sina, |
|
| and
components of a vector a, |
|
|
|
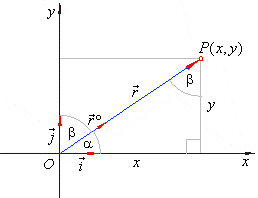 |
|
|
|
|
If a vector
a
in 3D space forms with the coordinate axes, x,
y and z
angles,
a,
b
and g
respectively, then
|
|
components of the vector are,
|
|
|
|
while for the radius vector of the point
P(x,
y, z),
|
|
|
| Therefore, for angles, a,
b
and g
hold the expressions,
|
|
|
| that are called the
directional cosines of the vector
a.
|
|
 |
|
|
|
|
The unit vector of the vector
a,
|
|
|
|
|
|
This condition must satisfy angles that a vector in three-dimensional space form with the coordinate axes.
|
|
For vectors in a coordinate plane
|
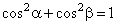 |
and since
b
= 90° -
a,
then |
|
|
| cosb
= cos(90°
-
a)
= sina,
follows |
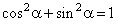 |
the basic trigonometric identity.
|
|
|
Similarly, the
unit vector of a radius vector
in
space
|
|
|
|
determined by corresponding directional
cosines.
|
|
Therefore the radius vector forms with coordinate axes
angles,
|
|
|
|
As vectors are uniquely determined by its components or coordinates, they are usually denoted using
matrix algebra notation,
|
|
in the coordinate plane,
|
 |
| and in the 3-D
space |
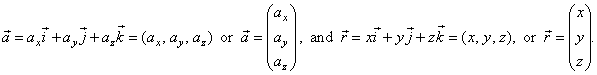 |
|
|
Vectors in
a three-dimensional coordinate system, examples |
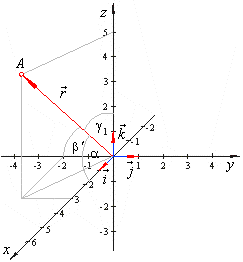
| Example:
Determine angles that a radius vector of the point
A(3,
-2, 5) forms with the coordinate axes. |
| Solution:
Let calculate the magnitude or length of the radius vector, |
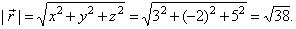 |
| Angles between the radius vector and the coordinate axes are, |
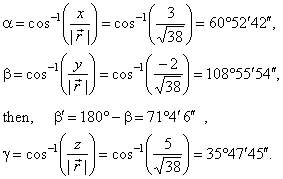 |
|
 |
|
|
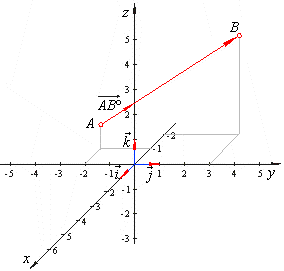
| Example:
A vector AB is directed from point
A(-1,
-2,
1) to point B(-2,
3, 4), find the unit vector of the
vector AB. |
| Solution:
Determine the vector AB
from the expression |
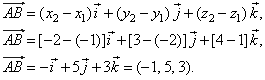 |
| The length of the vector
AB |
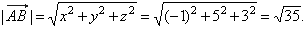 |
| The unit vector of the vector
AB |
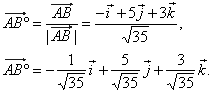 |
|
 |
|
| Check
that the directional cosines of the unit vector satisfy the relation, |
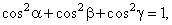 |
|
|
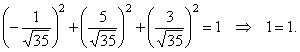 |
|
|
Example: A vector
a
in a 3D-space, of the length | a
|
= 4, forms with axes,
x and
y
the same angles, |
| a
= b
= 60°, find the
components (coordinates) of the vector a. |
| Solution:
Using relation |
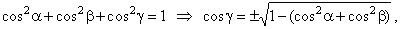 |
|
|
| applying given conditions, |
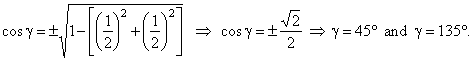 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| College
algebra contents
F |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |