|
|
|
Systems
of Linear Inequalities
|
Solving and graphing systems of
linear inequalities
|
|
Solving and graphing systems of
linear inequalities in two variables
|
|
|
Rational
Inequalities |
|
Method of
solving rational inequalities
|
|
|
|
|
|
|
|
|
Systems
of Linear Inequalities
|
| The solution of the system of
simultaneous inequalities is the intersection of sets
of the individual solutions.
|
| Example:
Solve and graph the
solution of the given system of simultaneous inequalities.
|
|
|
 |
|
 |
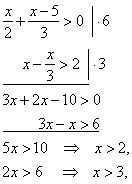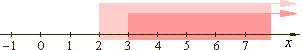| the solution of the system
is the open interval (3, +
oo ). |
|
|
|
|
Solving and graphing systems of
linear inequalities in two variables
|
|
The set of points whose coordinates (x,
y)
satisfy the inequality ax+
by + c > 0 is a
half-plane of a Cartesian plane.
|
| Example:
Solve and graph the
solution of the given system of linear inequalities in two
variables.
|
|
Solution:
|
 |
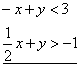| Plug the
coordinates of the origin |
 |
|
|
 |
|
|
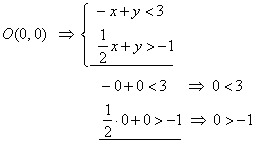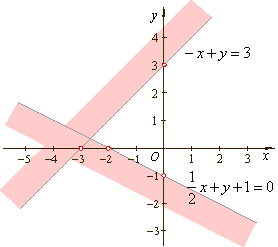Thus, non shaded area of the Cartesian
plane where lies the origin, bounded by given lines, is the solution of the system of inequalities.
|
|
|
|
Rational
Inequalities
|
|
A rational inequality can be written
in one of the following standard forms:
|
|
P/Q > 0
or
P/Q < 0
(or
P/Q > 0
or P/Q < 0), where
Q
is not 0.
|
|
The sign of the rational expression
P/Q, where
P
and Q
are polynomials, depends on the signs of P
and
Q.
|
|
As the signs of the
polynomials change at the zeros, to solve a rational inequality we should find the zeros of
both P
and Q
first and then we can determine the intervals of the independent variable that satisfy given rational inequality.
|
|
|
|
Method of solving
rational inequalities
|
|
The first step to solve a rational
inequality is to get a single rational inequality on the left side
of the inequality sign and have zero on the right side of the
inequality sign.
|
|
The next step is to factor the numerator and denominator and find the values of
x
that make these factors equal to 0 to find critical points (boundaries, endpoints of intervals).
|
|
Note that, by setting the numerator to
0 we get the zero points of the given rational expression, but by setting the denominator
to 0 we get points at which the rational expression or function is undefined
(i.e., when plugged into the expression give division by zero).
|
|
The rational functions are not defined at the zeros of the denominator. Therefore, they have breaks or vertical asymptotes at these points,
and this is why these points cannot be included into the solution of the rational inequality.
|
|
|
| Example:
Solve the rational
inequality
|
 |
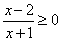and
draw the graph of the rational function. |
|
|
Solution:
The solution set of the given rational inequality includes all
numbers
x
which make the inequality greater then or equal to 0, or which make the sign of the rational expression
to be positive or 0.
|
|
A rational expression is positive if both the numerator and the denominator are positive
or if both are negative, and the rational expression equals 0 when
its numerator is equal to 0 that is
|
|
|
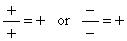
therefore, we have to solve two simultaneous
inequalities:
|
|
|
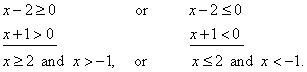
The solutions represented on the
number line are shown below.
|
|
|
Thus, the solution set of the given
inequality written in the interval notation is (-
oo,
-1)
U
[2, oo ).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
College
algebra contents C
|
|
 |
|
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
