|
|
|
Simultaneous
Linear Equations
|
 System of two linear equations in
two unknowns (variables)
System of two linear equations in
two unknowns (variables)
|
|
The
system has, a single solution, no solution or has infinitely many
solutions
|
|
Solving
systems of equations
|
 Substitution and comparison
method
Substitution and comparison
method
|
 Addition or elimination method
Addition or elimination method
|
|
|
|
|
|
|
| System of two linear equations in
two unknowns (variables)
|
| Two linear equations in two unknowns
x,
y
form a system if they can be written in the standard form: |
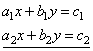 |
| that is, in the form where the variables in both equations are in
order on the left side and the constant term c
is on the right.
|
| The
numbers, a1
and a2,
are the coefficients of the x
variable and, b1 and
b2, are
the
coefficients of the y
variable. |
| Underlying indicates that the two
equations should be solved simultaneously.
|
| The solution of a linear equation in two unknowns is every ordered pair of numbers
(x,
y), when substituted into equation, satisfy the equation. |
| All
these ordered pairs of numbers are the points of the strait line in a
coordinate plane. Therefore, simultaneous equations can be solved
graphically. |
| The solution of the system of equations, are the values
of the variables that make both equations true at the same time. |
|
Graphically it is the intersection point of the two lines, because the
intersection point is the only point that lies on both lines at the same
time. |
|
| The
system has, a single solution, no solution or has infinitely many
solutions
|
| The following three cases are possible for any given system
of linear equations: |
| a) The system has a single solution, lines intersect, and the
coordinates (x,
y)
of the intersection point are the one and only solution to the system of equations.
|
| In this case the ratios of the
coefficients of the unknowns x,
y
are not equal, |
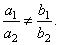 |
|
|
| In
this case the system of equations is called independent system.
|
|
b) The system has no solution.
|
| Graphically, lines are parallel, i.e.,
have the same slope, but are not identically the same line and they
will
|
| never intersect, that is:
|
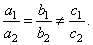 |
|
|
| Equations are said to
be inconsistent.
|
| c) The system has infinitely many solutions. Equations describe the
same line.
|
|
The three ratios are equal:
|
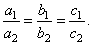 |
|
|
| This is called
dependent system.
|
|
|
| Solving
systems of equations
|
| When solving a system of simultaneous equations in two unknowns,
we use algebraic methods to get such equivalent system at which one of two equations will contain only one variable.
|
| Then, solve that
equation, and substitute its solution in another equation. That way,
this equation also turns into a single equation with a single unknown.
|
|
Finish by solving that single equation.
|
|
|
| Substitution and comparison method
|
| With the substitution method, we solve one of the equations for one
variable in terms of the other, and then substitute that into the other
equation.
|
| Example:
Solve the system of
equations.
|
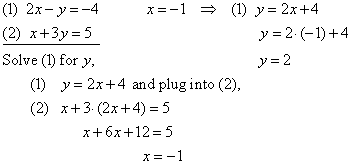
|
|
Similar is the comparison method.
|
|
Solve both equations for the
same variable in terms of the other, and then compare them, as is
shown in the example.
|
| Example:
Solve the system of
equations using comparison method.
|
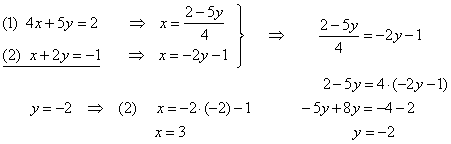
|
|
|
|
Addition or elimination method
|
|
To eliminate one of the variables from either of equations to obtain
an equation in just one unknown, make one pair of coefficients of
the same variable in both equations negatives of one another by multiplying both sides of an equation by the same number.
|
|
Upon
adding the equations, that unknown will be eliminated.
|
| Example:
Solve the system of
equations using elimination method.
|
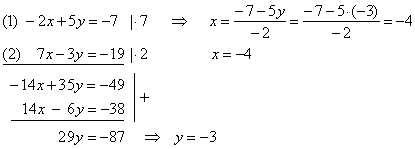
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
College
algebra contents C
|
|
 |
|
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |