| |
|
|
Rectangular
(Two-dimensional, Cartesian) Coordinate System |
Coordinate axes, x-axis
and y-axis,
origin, quadrants
|
|
Points in the
Coordinate plane |
|
Midpoint of a line segment
|
|
The distance formula
|
|
Dividing
a line segment in a given ratio |
|
The
area
of a triangle |
|
The
coordinates of the centroid of a triangle |
|
Lines
parallel to the axes, horizontal and vertical lines
|
|
|
|
|
|
|
| Coordinate axes, x-axis
and y-axis,
origin, quadrants
|
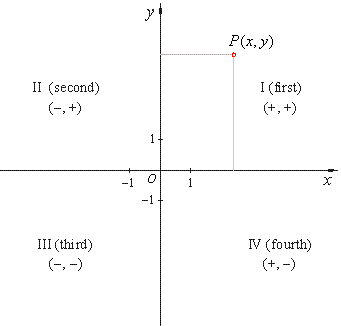
| The Cartesian coordinate system is defined by two
axes at right angles to each other, forming a plane. |
| The horizontal axis is
labeled x, and the vertical axis is labeled
y. |
| The point of intersection,
where the axes meet, is called the origin labeled
O. |
| Given each axis,
choose a unit length, and mark off each unit along the axis, forming
a grid. |
| The position of each point in a plane is identified with an
ordered pair of real numbers, in the form (x,
y), called the
coordinates of the point. |
| The
x-coordinate, called the
abscissa, equal to the distance of the point from the y-axis measured parallel
to the x-axis.
|
| The
y-coordinate, called the
ordinate, is the distance of the point from the x-axis measured parallel to the
y-axis.
|
| The
origin O
has coordinates (0,
0). |
| The intersection of the two axes creates four quadrants
indicated by numerals I, II, III, and IV. |
| The quadrants are labeled
counterclockwise starting from that in which both coordinates are
positive. |
 |
|
| Midpoint of a line segment
|
| The
point on a line segment that is equidistant from its endpoints
is called the midpoint. |
| The coordinates of the midpoint
M (xM,
yM)
of the line segment P1P2
where, P1(x1,
y1)
and P2(x2,
y2)
are endpoints, |
|
|
|
|
|
| Example:
Find the midpoint of the
line segment AB
where the endpoints, A(-5,
3)
and B(-1,
-1). |
|
|
|
| The distance formula
|
| The
distance between two given points in a coordinate
(Cartesian) plane. |
|
|
|
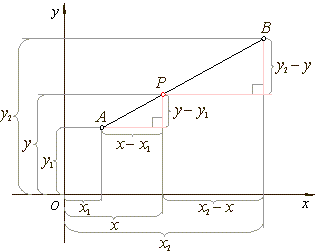
| Dividing a line segment in a given ratio
|
| A
given line segment AB
in a Cartesian plane can be divided by a point P
in a fixed ratio, internally or externally. |
| If
P
lies between endpoints then it divides AB
internally. If P
lies beyond the endpoints A
and B
it divides the segment AB
externally. |
| The
ratio of the directed segments l
=
AP
:
BP |
| is
negative in the case of the internal division since the segments
AP
and BP
have opposite sense, while in the external division, the ratio l
is positive. |
 |
|
| As
l
=
AP
:
BP |
| and
shown triangles are similar, then |
 |
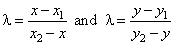| which,
with l
negative, gives |
|
|
| the coordinates of
the point P. |
| |
|
|
|
| Example:
The line segment, with
endpoints A(-3,
5)
and B(6, -1),
is divided by a point P
internally in the ratio l
= AP
: BP
= 1 : 2. Find the coordinates
of the dividing point P. |
| Solution: |
|
 |
|
|
|
|
|
|
|
 |
|
|
|
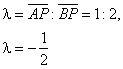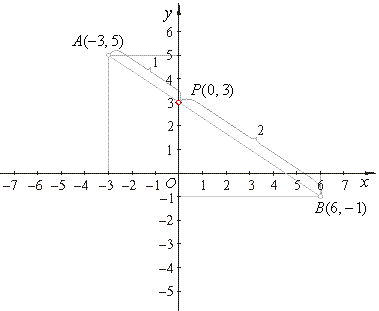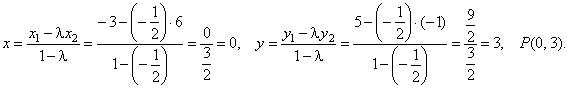
| The
area
of a triangle |
| The
rectangular coordinates of three points in a coordinate plane
describe a triangle. Using given coordinates we derive the
formula for the area of the triangle, as is shown in the diagram
below. |
 |
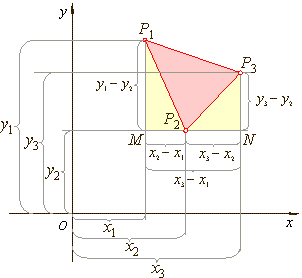| The
area of the given triangle P1P2P3
equals |
| the
area of the trapezium P1MNP3
minus
the |
| sum
of the areas of the right triangles, P1MP2
and |
| P2NP3,
that is |
| PD =
1/2·[(y1 -
y2)
+ (y3 -
y2)]
· (x3 -
x1)
- |
| -
1/2·[(y1
- y2)·(x2
- x1)
+ (y3 -
y2)·(x3
- x2)] |
| which
after simplifying and rearranging gives |
| PD=1/2·[x1(y2
- y3)
+ x2(y3 -
y1)
+ x3(y1 -
y2)] |
|
|
|
| Example:
Two vertices of a triangle
lie at points A(-4,
0)
and B(5, -2)
while third vertex C
lies on the y-axis.
Find the coordinates of the point C
if the area of the triangle is 31 square units. |
| Solution: |
|
 |
|
|
|
|
|
 |
|
|
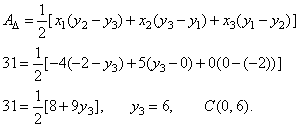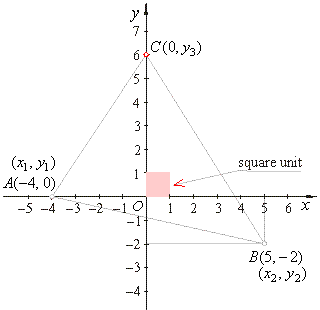| The
coordinates of the centroid of a triangle |
| The
point of coincidence of the medians of a triangle is called the centroid. |
| The
median is a straight line joining one vertex of a triangle to
the midpoint of the opposite side and divides the triangle into
two equal areas. |
| The
centroid cuts every median in the ratio 2
: 1 from a vertex to the
midpoint of the opposite side. |
| The
coordinates of the centroid of a triangle given its three
points, P1, P2 and
P3
in a coordinate plane: |
| The
centroid M(x,
y),
where |
x
= 1/3 · (x1 + x2
+ x3), y =
1/3 · (y1
+ y2
+ y3) |
|
|
|
| Lines
parallel to the axes, horizontal and vertical lines
|
| If
the y
value never changes, i.e., if it takes the same constant value
y =
c
a line is parallel to the
x-axis
and is called a horizontal line (or constant). |
| If
the x
value never changes, i.e., if it takes the same constant value
x
=
c a line is parallel to the y-axis
and is called a vertical line. |
|
 |
|
|
|
|
|
|
|
|
|
|
|
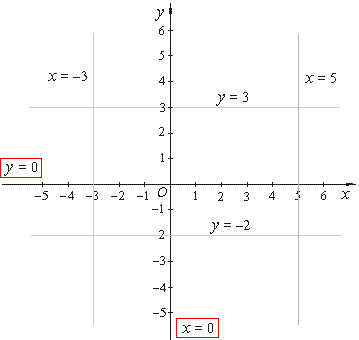College
algebra contents A
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
