| |
|
|
|
Radicals
(roots) and/or exponentiation
with fractional (rational) exponent
|
 Rules and properties of radicals
Rules and properties of radicals
|
 Rules and properties of radicals
and/or fractional exponents
Rules and properties of radicals
and/or fractional exponents
|
 Simplifying radical expressions
Simplifying radical expressions
|
|
|
|
|
|
|
|
|
|
|
Radicals
(roots) and/or exponentiation
with fractional (rational) exponent
|
| The
nth
root of a real number a,
denoted |
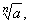 |
is defined
to be that number x
such that xn
=
a,
i.e., |
|
| |
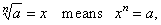 |
where
n
is a natural number greater than 1. |
|
| Thus, if a
= 0,
then |
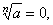 |
|
|
|
if a
> 0,
then |
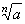 |
is the positive real number
x such
that xn
=
a, |
|
|
if a
< 0
and n
is odd, then |
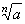 |
is the negative real number
x such
that xn
=
a, |
|
|
if a
< 0
and n
is even,
then |
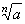 |
is not a real number,
|
|
|
if n
is an even number, the nth
root of a
is defined to be that
number x
≥ 0 such that xn
=
a.
|
|
Even roots exist only
for nonnegative numbers.
|
| |
Odd
roots always exist and have the property that |
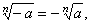 |
where n
is odd.
|
|
|
The expression |
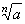 |
is called a
radical, the number a
is called the radicand, and n
is the index of the
|
|
| radical. The symbol |
 |
is called the radical
sign.
|
|
|
The principal nth
root of a real number a
is the unique real number x
which is an nth
root of a
and is of the same sign as a.
|
|
|
|
Rules and properties of radicals
|
|
Let n
be a natural number
and a
be a real number, then
|
| 1. |
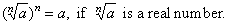 |
|
| 2. |
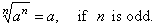 |
|
| 3. |
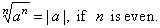 |
|
|
|
| Examples: |
1. The odd root of any real number exists: |
|
| a) |
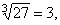 |
since
33
= 27. |
| b) |
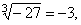 |
since
(-3)3
= (-3)·(-3)·(-3)
= -
27. |
| c) |
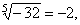 |
since
(-2)5
= (-2)·(-2)·(-2)·(-2)·(-2)
= -32. |
|
| |
2.
The
even root of a nonnegative real number exists: |
|
| a) |
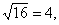 |
since 42
= 16 and 4
> 0, [recall
that ( ±
4)2
= 16]. |
| b) |
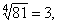 |
since 34
= 81 and 3
> 0, [recall
that ( ±
3)4
= 81]. |
|
|
Note that the even root is defined to be a nonnegative
number. |
|
| |
3.
The
even root of a negative real number does not exist as a real
number. |
|
| For example, |
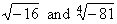 |
do
not exist as real numbers, but they do exist as complex
numbers. |
|
|
|
|
Rules and properties of radicals
and/or fractional exponents
|
|
If
m,
n and p
are natural numbers
(n
>1) and
if a
and b
are nonnegative
real numbers, then |
| Properties |
|
Examples |
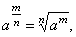 |
|
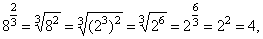 |
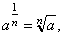
|
|
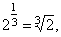 |
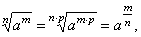 |
|
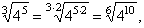 |
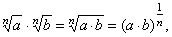 |
|
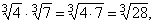 |
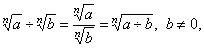 |
|
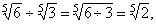 |
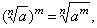 |
|
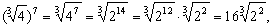 |
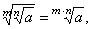 |
|
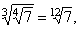 |
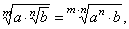 |
|
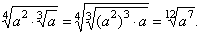 |
|
|
|
|
Simplifying radical expressions
|
|
As,
to simplify means to reduce given expression to a simpler form, or find another expression with the same
value. So, for example a square root radical expression is simplified when its radicand has no square factors.
|
|
To simplify a radical means to
remove factors from the radical until no factor in the radicand
has an exponent greater than or equal to the index of the radical
and the index is as low as possible.
|
|
Therefore, use the product rule of
radicals to simplify the
nth root radicals.
Throughout,
we take variables to be positive, unless the index of the
radical is odd.
|
|
|
|
|
|
|
|
|
|
|
|
|
| College
algebra contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
|
|