|
|
|
| The principal square root function
- the inverse of the square of x
(or quadratic) function |
| Definition
of the inverse function |
| The
inverse function is a function, usually written f
-1,
whose domain and range are respectively the range and
domain of a given function f,
that is |
| |
f
-1(x)
= y if
and only if f
(y)
= x, |
|
|
| or it is
the function whose composition with the given function
is the identity function, i.e., |
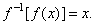 |
|
|
|
|
|
|
|
| In
order that the inverse should have a unique value for each
argument, and so be properly a function, the
extraction of positive square roots
is the inverse of squaring, since |
|
|
| however,
without the restriction to positive values, the square root
function on the domain of real numbers does not have an inverse. |
|
| The
graph of the principal square root function |
| The
graph of the inverse function is the reflection about the line y =
x
of the graph of a given function. |
| A
function f has an inverse if and only if when its graph is
reflected about the line y =
x, the result is the graph of a
function that passes the vertical line test. |
| A
relation is a function if there are no vertical lines that
intersect the graph at more than one point. |
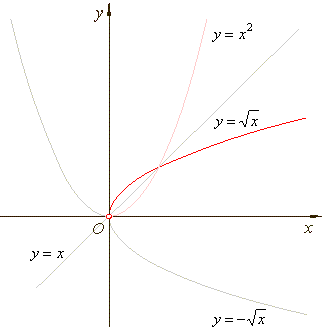 |
|
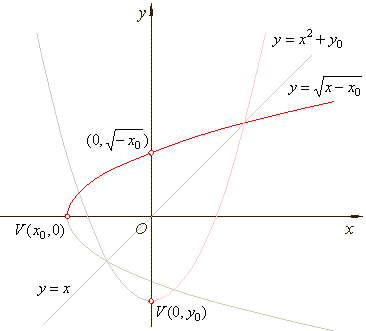
| Translation of the principal square root function
in the direction of
the x-axis |
| Horizontal
line test |
| A
function f
has an inverse if no horizontal line intersects the graph of f
more than once. |
| If
any horizontal line intersects the graph of f
more than once, then f
does not have an inverse. |
| A
mapping associating a unique member of the codomain with every
member of the domain of a function is called one to one
correspondence. |
| A
function f
is one-to-one if and only if f
has an inverse. |
| Given
f
(x)
= x2 + y0
and,
since f
[f
-1(x)]
= x |
|
therefore, f
[f
-1(x)]
= [f
-1(x)]2
+ x0
= x, or
[f
-1(x)]2
= x -
x0
|
| then |
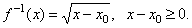 |
|
|
| To find the
y-intercept,
set x
= 0 and solve for y, that is, |
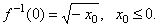 |
|
|
| The
graph of
translated principal square root function
in the direction of
the x-axis |
 |
|
|
|
|