|
| Sigma
notation of the polynomial |
| Coefficients of the source
polynomial in the form of a recursive formula
|
| According
to mathematical induction we can examine any
n-degree
polynomial function using shown method. |
| Therefore,
the polynomial f
(x) =
y = anxn
+ an-1xn-1
+ an-2xn-2
+ .
. .
+
a2x2
+
a1x + a0 |
| we can
write as
|
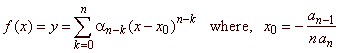 |
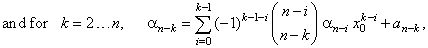 |
|
while, for k = 0, an
=
an, |
|
|
|
and from an-k, for
k =
n,
a0
=
f
(x0)
= y0. |
| |
| Thus,
expanded form of the above
sum is |
| y
- y0
= an(x
- x0)n
+ an-2(x
- x0)n-2
+ .
. .
+
a2(x
- x0)2
+ a1(x
- x0) |
| where
x0
and y0
are coordinates of translations
of the graph of the source polynomial |
| fs(x)
= anxn
+ an-2xn-2
+
.
. .
+
a2x2
+ a1x
|
| in
the direction of the x-axis
and the y-axis
of a Cartesian coordinate system. |
| Therefore,
every polynomial written in the general form can be
transformed into translatable form by calculating the
coordinates of translations x0
and y0
and the coefficients a
of its source function. |
| Note
that the complete source polynomial has n
-
1 terms, missing
second and the absolute term. |
|
| Coefficients
of the source polynomial function are related to its derivative
at x0 |
| The
coefficients of the source polynomial are related to
corresponding value of its derivative at x0
like the coefficients
of the Taylor polynomial in Taylor's or Maclaurin's formula,
thus |
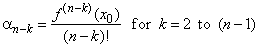 |
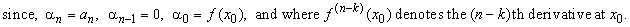 |
|
| Such
for example, the coefficient a1
of the source cubic of
f (x) =
a3x3
+
a2x2
+
a1x + a0 |
| since
f ' (x)
=
3a3x2
+ 2a2x
+
a1
and x0
=
-
a2/(3a3)
then |
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
College
algebra contents C
|
|
 |
|