|
|
|
| Polynomial and/or Polynomial
Functions and Equations |
 Definition
of a polynomial or polynomial
function
Definition
of a polynomial or polynomial
function |
 Division
of polynomials
Division
of polynomials |
 Factoring
polynomials and solving
polynomial equations by factoring
Factoring
polynomials and solving
polynomial equations by factoring |
|
Solving quadratic and
cubic equations by factoring, examples |
|
|
|
|
|
|
| Definition
of a polynomial or polynomial function |
| A
polynomial and/or polynomial function in the variable x
is an expression of the general (or standard) form |
| f
(x)
= anxn
+ an-1xn-1
+ . . .
+
a1x
+ a0 |
| consisting
of n
+ 1 terms each of which is a product of a real coefficient ai
and the variable x
raised to a non-negative
integral power. |
| If
the leading coefficient of a polynomial an
is
not
0
then, the
degree of the polynomial is n. |
|
The constant term a0
is the y-intercept
of the polynomial. |
|
| Division of polynomials
|
| Dividing two polynomials,
p (x) and
q (x)
obtained is quotient Q
(x)
and remainder R (x),
that we write as |
|
p (x)/q (x)
= Q (x) + R (x)/q (x)
or
p (x)
= Q
(x)
· q
(x)
+ R (x). |
| Two polynomials are divisible if
R (x)
= 0. |
| Divide
the highest degree term of dividend by the highest degree term
of the divisor to get the first term of the quotient. |
| Take the first term of the quotient and multiply it by every term of divisor.
Write this result below the dividend, making sure you line up all the terms with the terms of the dividend that has the same degree. |
| Subtract the result from the dividend, i.e., reverse all the signs of the terms of the result and add like terms. |
| Repeat the process of long division until the degree of the new obtained dividend is less than the degree of the divisor. |
|
|
| Note,
since each second line should be subtracted, the sign of each term is reversed. |
|
|
b)
(
3x4 +
x2 +
5) ¸
( x2 -
x -
1) |
|
|
|
|
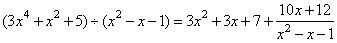 |
|
| |
|
| like |
17 ¸
5 = 3 +
2/5 |
| |
-15 |
| |
2 |
|
|
|
| Factoring
polynomials and solving
polynomial equations by factoring |
| A
polynomial and/or polynomial
function with
real coefficients can be expressed as a product of its leading
coefficient an
and
n
linear factors of the form x
-
xi,
where xi
denotes its real roots and/or complex
roots, |
| f
(x)
= anxn
+ an-1xn-1
+ . . .
+
a1x
+ a0
= an(x
- x1)(x
- x2)
.
. . (x
- xn).
|
| By
multiplying the parentheses on the right side and collecting
like terms and then comparing the resulting coefficients with
the coefficients of the given polynomial obtained are Vieta's
formulas that show relations between coefficients and roots of a
polynomial. |
| Thus, a quadratic or a second
degree polynomial |
|
a2x2
+ a1x
+ a0 = a2(x
- x1)(x
- x2)
= a2[x2
-
(x1 +
x2)x
+
x1x2], |
|
|
|
| and
similarly a cubic or a third
degree polynomial |
| |
a3x3
+ a2x2
+ a1x
+ a0 = a3(x
- x1)(x
- x2)(x
- x3)
= |
|
|
| |
=
a3[x3
-
(x1 +
x2
+
x3)x2
+
(x1x2 +
x1x3
+
x2x3)x
- x1x2x3]. |
|
|
| Solving quadratic and
cubic equations by factoring, examples |
|
Example:
|
Factorize (2/3)x2
- (2/3)x
- 4
using
the above theorem. |
| Solution: |
(2/3)x2
- (2/3)x
- 4
=
(2/3)(x2
- x
- 6)
=
(2/3)[x2
- (3
+ (-
2))x
+ 3(-
2)] |
|
= (2/3)(x2
- 3x
+ 2x
- 6)
=
(2/3)[x(x
- 3)
+ 2(x
- 3)]
=
(2/3)(x
- 3)(x
+ 2) |
|
|
| Example:
Given
are leading
coefficient a2
=
-1and
the pair
of conjugate complex
roots,
x1 =
1 +
i
and |
|
x2
=
1 - i,
of
a second
degree polynomial, find
the polynomial using
the above theorem. |
| Solution: |
By
plugging the given values into a2x2
+ a1x
+ a0 = a2(x
- x1)
(x
- x2) |
|
a2x2
+ a1x
+ a0 = -1[x
-
(1
+ i)]
· [x
-
(1 - i)]
= -[(x
- 1)
- i]
· [(x - 1)
+ i]
|
|
= -[(x - 1)2
- i2]
=
-(x2
- 2x
+ 1 +
1)
=
- x2
+ 2x
- 2 |
|
|
|
Example:
|
The
real root of the polynomial -
x3
-
x2
+ 4x
- 6
is
x1 =
- 3,
factorize the polynomial. |
| Solution: |
We
divide given polynomial by one of its known
factors, since |
|
a3x3
+ a2x2
+ a1x
+ a0 = a3(x
- x1)
(x
- x2)
(x
- x3) |
|
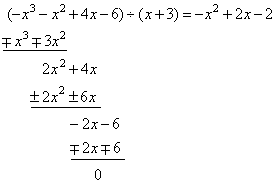 |
|
then
we calculate another two roots of given cubic by solving
obtained quadratic trinomial, |
|
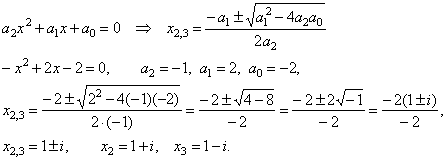 |
|
Finally
we use the theorem to factorize given polynomial (see
the previous example), |
|
a3(x
- x1)(x
- x2)(x
- x3)
= -1(x
+ 3)[x
-
(1
+ i)][x
-
(1 - i)]
= -1(x
+ 3)(x2
- 2x
+ 2). |
|
Notice that given cubic has one real root and the pair of the conjugate complex roots. |
|
Odd
degree polynomials must have at least one real root. |
|
|
| Example:
Solve polynomial
equation x3
+ 2x2 -
x -
2 = 0 by factoring. |
| Solution:
x2(x
+ 2) -
(x + 2) = 0 |
|
(x +
2)·(x2 -
1) = 0 |
|
(x +
2)·(x + 1)·(x -
1) = 0 |
|
x +
2 = 0 =>
x1 = -2 |
|
x +
1 = 0 =>
x2 = -1 |
|
x -
1 = 0 =>
x3 = 1 |
| The
roots are, x1
= -2,
x2 = -1
and x3
= 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
College
algebra contents C
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |