|
| Combinatorics -
Combinatorial
Analysis |
|
|
|
Variations |
Variations with repetition (or permuted
combinations with repetition) |
|
Variations with repetition (or permuted
combinations with repetition) examples |
|
|
|
|
|
|
| Variations with repetition (or permuted
combinations with repetition) |
| The number of ways to
choose r
objects from a set of n
different objects when order is important and one object can be chosen
more than once |
|
|
|
| Variations with repetition (or permuted
combinations with repetition) examples |
| Example:
Find the number of
variations with repetition of size 4 that
can be made from digits 0, 1, 2 and write them out. |
|
Solution: Since,
n = 3 and r
= 4 then the total number of
the variations with repetition
is |
 |
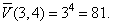| As
in the above example, first we should select all combinations
with repetition of size 4 from the 3 given digits, and then
write the permutations of each of them. |
| Let
calculate the number of combinations |
 |
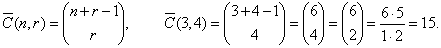| The
15 distinct combinations are divided into four groups depending
on the number of permutations each |
| group yields, |
|
a |
|
b |
|
c |
|
d |
|
|
0
0 0 0 |
|
0
0 0 1 |
|
0
0 1 1 |
|
0
0 1 2 |
|
|
1
1 1 1 |
|
0
0 0 2 |
|
0
0 2 2 |
|
1
1 0 2 |
|
|
2
2 2 2 |
|
1
1 1 0 |
|
1
1 2 2 |
|
2
2 0 1 |
|
|
|
|
1
1 1 2 |
|
|
|
|
|
|
|
|
2
2 2 0 |
|
|
|
|
|
|
|
|
2
2 2 1 |
|
|
|
|
|
|
| The
3 combinations from the group a
can not be rearranged. |
|
Each combination from the group b,
c
and d,
gives, |
|
|
| as
they are the permutations
of the 4 objects some of which are the
same. |
| Thus,
the permuted combinations (or the variations) of the group b
are, |
| 0
0 0 1 0
0 0 2 1 1 1
0 1 1 1 2 2 2 2
0 2 2 2 1 |
| 0
0 1 0 0
0 2 0 1 1 0
1 1 1 2 1 2 2 0
2 2 2 1 2 |
| 0
1 0 0 0 2 0 0 1
0 1 1 1 2 1 1 2
0 2 2 2 1 2 2 |
|
1 0 0 0 2 0 0 0
0 1 1 1 2 1 1 1
0 2 2 2 1 2 2 2 ( 6 ´
4 =
24 variations) |
|
|
the variations of the group c
are,
the variations of the group d
are, |
|
0 0 1 1 0
0 2 2 1 1 2 2
0
0 1 2 1 1 0 2
2 2 0
1 |
|
0 1 0
1 0 2 0 2 1 2 1 2
0
0 2 1 1 1 2
0 2 2 1 0 |
|
0 1 1
0 0 2 2 0 1 2 2
1
0 1 0 2 1 0 1 2
2 0 2 1 |
|
1 1 0
0 2 2 0 0 2 2 1
1
0 1 2 0 1 0 2 1
2 0 1 2 |
|
1 0 1
0 2 0 2 0 2 1 2
1
0 2 0 1 1 2 1 0
2 1 2 0 |
|
1 0 0
1 2 0 0 2 2 1 1 2
0 2 1 0 1 2 0 1
2 1 0 2 |
|
( 3 ´
6 =
18 variations)
1 0 0 2 0 1 1 2
0 2 2 1 |
|
1 0 2 0 0 1 2 1
0 2 1 2 |
|
1 2 0 0 0 2 1 1
0 1 2 2 |
|
2 0 0 1 2 1 1 0
1 2 2 0 |
|
2 0 1 0 2 1 0 1
1 2 0 2 |
|
2 1 0 0 2 0 1 1
1 0 2 2 |
|
( 3 ´
12 =
36 variations) |
|
| Therefore,
the total number of the variations of size 4 with repetition
chosen from the given 3 digits are, |
| V(3,
4) = 3 + 6 ´
4 + 3 ´
6 + 3 ´
12 = 3 · (1 + 8 + 6 + 12) = 3 · 27 = 3 · 33 = 34
= 81. |
|
| Example: Find the number of
variations with repetition of size 8 that
can be made from the binary digits 0, 1. |
|
Solution: Since,
n = 2 and r
= 8 then the total number of
the variations with repetition is |
| V(n,
r) = nr
=> V(2, 8) =
28 = 256. |
| First
we should select the combinations of size 8 that
can be made from the 2 binary digits, then examine |
| the number of
ways each combination can be rearranged or permuted to prove the
total number of variations. |
| So,
the number of the combinations is |
 |
| The
9 combinations are, |
| 1) |
|
|
this
combination can not be rearranged or permuted |
| 2) |
|
|
this
combination can not be rearranged or permuted |
| 3) |
|
|
 |
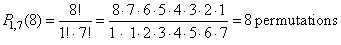| 4) |
|
|
 |
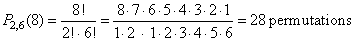| 5) |
|
|
 |
| 6) |
|
|
 |
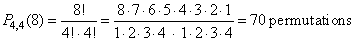| 7) |
|
|
|
| 8) |
|
|
|
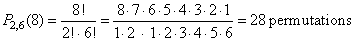| 9) |
|
|
|
|
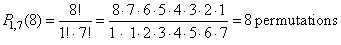| Therefore,
the total number of the variations of size 8 with repetition
chosen from the given 2 digits are, |
| V(2,
8) = 2 + 2 ´
8 + 2 ´
28 + 2 ´
56 + 70 = 2 · (1 + 8 + 28 + 56 + 35) = 2 · 128 = 2 · 27 =
28 |
| V(2,
8) = 28 = 256. |
| Both
numerical and nonnumerical data can be processed by the computer
as all letters digits and special characters are coded
(represented as a unique sequence of binary digits 0 and 1)
using binary variations. |
|
|
|
|
|
|
|
|
|
|
|
College
algebra contents
G
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
