|
| Combinatorics -
Combinatorial
Analysis |
|
|
|
|
Combinations
|
Combinations
|
|
Combinations
with repetition
|
|
|
Variations |
|
Variations or permuted
combinations (permutations without repetition) |
|
|
|
|
|
|
| Combinations
|
| Given
a set of n
different elements or objects. Select a subset of r
elements out of n.
Such selection is |
| called the combination. |
| A
combination is an unordered arrangement of r
objects selected from n
different objects taken r
at a time. |
| The number of
distinct combinations selecting r
elements out of n
is |
|
|
| Therefore,
combinations must differ from each other at least in one element. |
|
| Example:
Find the number of
combinations of size 3 that
can be made from digits 1, 2, 3, 4,
5 and
write |
| them out. |
|
Solution: Since,
n = 5 and r
= 3 then |
 |
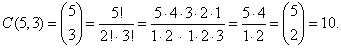| The
combinations are,
1 2 3 2
3 4 3
4 5. |
|
1 2 4
2 3 5 |
|
1 2 5
2 4 5 |
|
1 3 4 |
|
1 3 5 |
|
1 4 5 |
|
| Example:
Find the number of
combinations of size 4 that
can be made from letters A, B, C, D, E, F and |
|
write them out. |
|
Solution: Since,
n = 6 and r
= 4 then |
 |
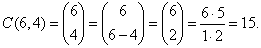| The
combinations are,
A B C D B
C D E C
D E F. |
|
A B C E
B C D F |
|
A B C F
B C E F |
|
A B D E
B D E F |
|
A B D F |
|
A B E F |
|
A C D E |
|
A C D F |
|
A C E F |
|
A D E F |
|
| Combinations
with repetition
|
| The number of ways to
choose r
objects from a set of n
different objects, so that an object can be chosen |
| more than
once |
|
|
| Remember
that combinations must differ from each other at least in one
element. |
|
| Example:
Find the number of
combinations of size 3 that
can be made from digits 1, 2, 3, 4 if repetition is |
| allowed, and
write them out. |
|
Solution: Since,
n = 4 and r
= 3 then |
 |
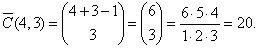| The
combinations are,
1 1 1 2
2 2 3
3 3 4
4 4 1 2 3 |
|
1 1 2 2
2 1 3
3 1 4
4 1 1 2
4 |
|
1 1 3 2
2 3 3
3 2 4
4 2 1 3 4 |
|
1 1 4 2
2 4 3
3 4 4
4 3 2 3 4 |
| |
| Example:
Find the number of
combinations of size 4 that
can be made from letters A, B, C if repetition is |
| allowed, and
write them out. |
|
Solution: Since,
n = 3 and r
= 4 then |
 |
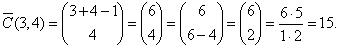| The
combinations with repetition are,
A A A A B
B B B C
C C C A
A B C |
|
A A A B B
B B C C
C C A B
B A C |
|
A A B B B
B C C C
C A A C
C A B. |
|
A B B B B
C C C C
A A A |
|
| Variations or permuted
combinations (permutations without repetition) |
| The
variations of size r
chosen from a set of n
different objects are the permutations of combinations of r. |
| The number of variations of size
r
chosen from n
objects equals the number of combinations of size r |
| multiplied
by the r!
permutations, |
|
|
|
| Example:
Find the number of
variations of size 3 that
can be made from digits 1, 2, 3, 4 and
write them out. |
|
Solution: Since,
n = 4 and r
= 3 then |
 |
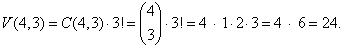| Notice
that there are 4 combinations of size 3 chosen from the given 4
digits, each of which gives six |
| permutations as is shown below. |
| The
variations are,
1 2 3 1
2 4 1
3 4 2
3 4 |
|
1 3 2 1
4 2 1
4 3 2
4 3 |
|
2 1 3 2
1 4 3
1 4 3
2 4 |
|
2 3 1 2
4 1 3
4 1 3
4 2 |
|
3 1 2 4
1 2 4
1 3 4
2 3 |
|
3 2 1 4
2 1 4
3 1 4
3 2. |
|
|
|
|
|
|
|
|
|
|
|
College
algebra contents
G
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
