Imaginary and complex numbers
      Exponentiation and root extraction of complex numbers in the polar form
         Powers and roots of complex numbers, use of de Moivre’s formulas examples
      Euler’s formula, relationship between trigonometric functions and the complex exponential function
Exponentiation and root extraction of complex numbers in the polar form - de Moivre's formula
We use the polar form for exponentiation and root extraction of complex numbers that are known as de Moivre's formulas.
  zn = rn · [cos(nj) + isin(nj)]  
 and   
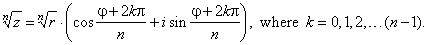Powers and roots of complex numbers, use of de Moivre’s formulas examples
Example: Compute    
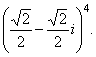Solution:  
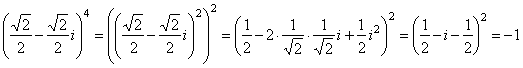or in the polar form,  
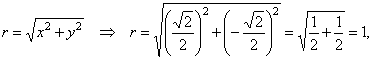and  
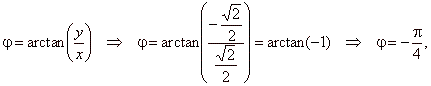since exponentiation with integer exponent  
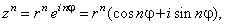then  
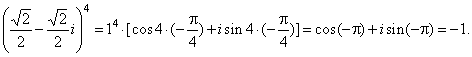Example: Compute    
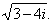Solution:  As square root of a complex number is a complex number, then
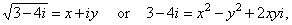and, two complex numbers are equal if their real parts are equal and their imaginary parts are equal, that is
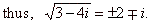Example: Calculate  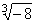 using de Moivre's formula.
Solution:
 
 
 
 
 
 
since
then
 
 
These complex numbers satisfy the equation z3 = -8 and by the Fundamental theorem of algebra, since this equation is of degree 3, there must be 3 roots.
Thus, for example to check the root zk=2 we cube this solution, 
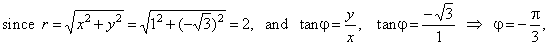then  
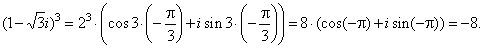Example: Calculate    
Solution:
 
 
 
 
 
 
 
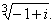Euler’s formula, relationship between trigonometric functions and the complex exponential function
Euler's formula
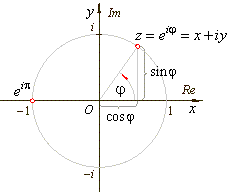
eij = cosj + isinj,  where
e is the base of the natural logarithm,
i is the imaginary unit, and
j is the angle between x-axis and the vector pointing to the complex number z measured counter clockwise, that is, j is the argument of z, 
describes the unit circle in the complex plane.
That is, on the unit circle lie points of the complex plane that correspond to the complex numbers each of which is one unit far from the origin.
Thus, by plugging the angles, 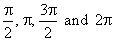into Euler's formula respectively  
obtained are the four complex numbers that lie on the unit circle, the two of which lie on the real axis and the two on the imaginary axis as shows the above picture.
The expression  eip + 1 = 0  is called Euler's equation or identity.
Euler's formula shows relations between trigonometric functions and complex exponentials.
Thus, by adding and subtracting Euler's formulas:
                                    (1)   eij = cosj + isinj
and                              (2)   e-ij = cos(-j) + isin(-j) = cosj - isinj
and solving for cosine and sine
 
 
 
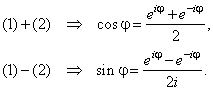We use Euler's formula to write complex number z = x + yi in polar coordinates,
  z = x + yi = r (cosj + isinj) = r eij  
where
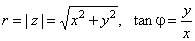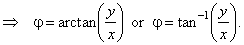College algebra contents
Copyright © 2004 - 2020, Nabla Ltd.  All rights reserved.