|
|
|
|
Imaginary
and complex numbers |
 Polar or trigonometric
notation of complex numbers
Polar or trigonometric
notation of complex numbers |
|
Multiplication
and division of complex numbers in the polar form |
|
Exponentiation
and root extraction of complex numbers in the polar form |
|
Powers and roots of
complex numbers, use of de Moivre’s formulas |
|
|
|
|
|
|
| Polar or trigonometric
notation of complex numbers |
| A point (x,
y)
of the complex plane that represents the complex number z
can also be specified by its distance r
from the origin and the angle j
between the line joining the point to the origin and the
positive x-axis. |
| Cartesian
coordinates expressed by polar coordinates: |
| x
= r cosj |
| y
= r sinj |
| plugged
into z
= x
+
yi
give |
|
z
= r
(cosj
+
isinj), |
|
| where |
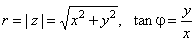 |
|
|
|
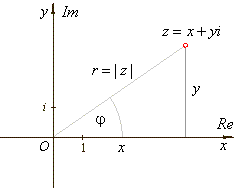 |
|
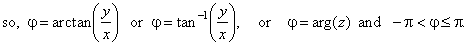 |
| Thus,
obtained is the polar or trigonometric form of a complex number
where polar coordinates are r,
called the absolute value or modulus, and j,
that is called the argument, written j
= arg(z). |
| By using
Euler's formula eij
= cosj
+
isinj,
a complex number can also be
written as |
| |
z
= r
eij |
which
is called the exponential form. |
|
|
| To show
the equivalence between the algebraic and the trigonometric form of a complex number, |
| z
= r
eij
= r
(cosj
+
isinj) |
| express
the sine and the cosine functions in terms of the tangent |
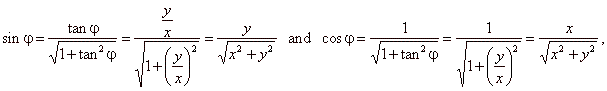 |
| and substitute
into above expression |
|
|
|
| Example: Given
the complex number z
= 1
-
Ö3i,
express z
= x
+
yi
in the trigonometric form.
|
| Solution:
The modulus |
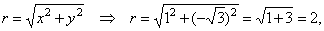 |
|
|
the argument |
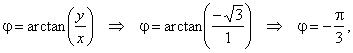 |
|
|
|
|
|
the trigonometric form is
|
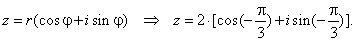 |
|
|
|
| Multiplication
and division of complex numbers in the polar form |
| If
given z1
= r1(cosj1
+ isinj1)
and z2
= r2(cosj2
+ isinj2)
then |
| |
z1
· z2 = r1
r2 · [cos(j1
+ j2)
+ isin(j1
+ j2)] |
|
|
| and |
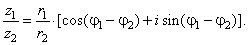 |
|
|
|
| Exponentiation
and root extraction of complex numbers in the polar form - de
Moivre's formula |
| We use the polar form
for exponentiation and root extraction of complex numbers that
are known as de Moivre's formulas. |
| |
zn
= rn · [cos(nj)
+ isin(nj)] |
|
|
| and |
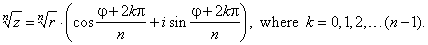 |
|
|
|
| Powers and roots of
complex numbers, use of de Moivre’s formulas examples |
| Example: |
Compute |
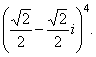 |
|
|
| Solution: |
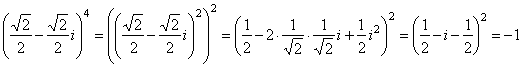 |
|
| or
in the polar form, |
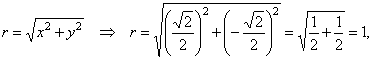 |
|
| and |
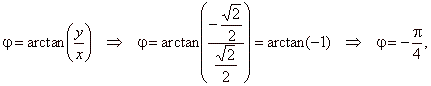 |
|
| since
exponentiation with integer exponent |
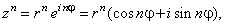 |
|
| then |
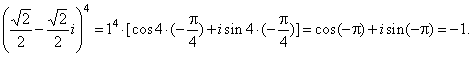 |
|
|
| Example: |
Compute |
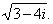 |
|
|
| Solution:
As square root of a
complex number is a complex number, then |
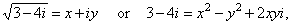 |
| and, two
complex numbers are equal if their real parts are equal and
their imaginary parts are equal, that is |
 |
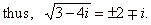 |
|
|
| Example: |
Calculate |
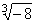 |
using de Moivre's
formula. |
|
|
|
|
|
|
|
| These complex numbers satisfy the equation z3
= -8
and by the Fundamental theorem of algebra, since this equation
is of degree 3, there must be 3 roots. |
| Thus, for
example to check the root zk=2
we cube this solution, |
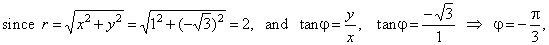 |
| then |
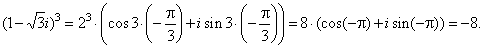 |
|
|
|
|
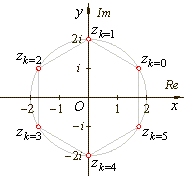
| Example: |
Calculate |
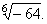 |
|
|
|
|
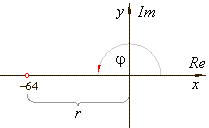
r
= 64 and
j =
p |
 |
|
| |
| |
| thus, |
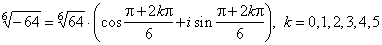 |
| |
|
 |
|
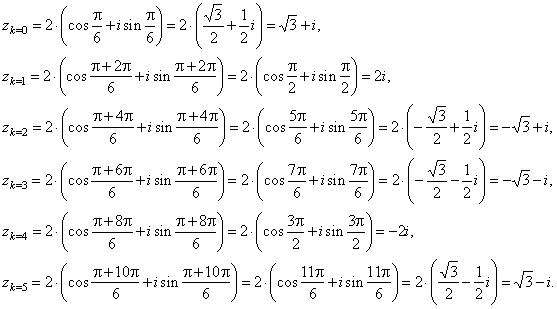 |
| These complex numbers satisfy the equation z6
= -64
and by the Fundamental theorem of algebra, since this equation
is of degree 6, there must be 6 roots. |
|
|
| Example: |
Calculate |
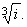 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
College
algebra contents
|
|
 |
|
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |