|
| Conic
Sections |
|
|
|
|
Circle
and Line
|
 Condition of tangency - Condition for a line to be the tangent to a circle
Condition of tangency - Condition for a line to be the tangent to a circle
|
|
Condition for a line to be the tangent to the circle with
the center at the
origin
O(0, 0)
|
|
Condition for a line to be the tangent to the translated circle
|
 Tangents to a circle from a point outside the circle - use of the
tangency condition
Tangents to a circle from a point outside the circle - use of the
tangency condition
|
|
|
|
|
|
|
| Condition of tangency - Condition for a line to be the tangent to a circle
|
| Condition for a line to be the tangent to the circle with center at the
origin
O(0, 0)
|
A line touches a circle if the distance of the center of the circle to the line is equal to the radius of the circle,
i.e., if d
= r. |
| The distance of the center
S(0,
0) of a circle
x2
+ y2 = r2
from a line y =
mx + c
or -mx
+ y -
c
= 0, |
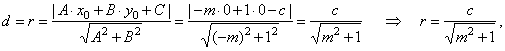 |
| and after squaring
obtained is |
r2·(m2
+ 1)
= c2 |
the condition for a line
y =
mx + c
to be a tangent to |
|
| the circle
x2
+ y2
= r2. |
|
| Condition for a line to be the tangent to the translated circle (x
-
p)2 + (y -
q)2 = r2 |
| In this case, the distance
d
of the center
S(p,
q) of the circle to a line
-mx
+ y -
c
= 0 (
or
y =
mx + c ),
must be equal to the radius r
of the circle, thus |
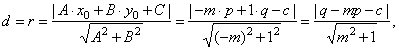 |
| after squaring
obtained is |
r2·(m2
+ 1)
= (q -m
p -
c)2 |
|
|
| the condition for a line
y =
mx + c
to be a tangent
to a translated circle with the center at S(p,
q). |
|
| We can derive the same conditions using
the tangency criteria which implies that the discriminant of the
system of equations of a line and a circle, in that case, must be zero. |
| Then will the system have only one solution, i.e., the line and the circle will have only one common point,
the tangency point. |
| 1)
The condition for a line y =
mx + c
to be tangent to the circle x2
+ y2
= r2, |
|
(1) y =
mx + c
plugging (1)
into (2)
gives the quadratic equation, |
|
(2) x2
+ y2 = r2
(m2
+ 1) · x2
+ 2mc · x
+ c2
-
r2
= 0 and
according to the condition, |
| |
| D
= b2
-
4ac = 0 or
(mc)2
- 4(m2
+ 1)(c2
- r2)
= 0 gives
r2·(m2
+ 1)
= c2
the tangency condition. |
|
| 2)
The condition for a line y =
mx + c
to be tangent to the circle (x
-
p)2 + (y -
q)2 = r2, |
|
(1) y =
mx + c |
|
(2) (x
-
p)2 + (y -
q)2 = r2 |
| |
| by
plugging (1)
into (2)
obtained is (m2
+ 1) · x2
+ 2(mc - mq
- p)
· x
+ p2
+ c2
+ q2 -
r2
-
2cq = 0 |
| then,
from the condition D
= b2
-
4ac = 0
follows
r2·(m2
+ 1)
= (q -m
p -
c)2
the
tangency condition. |
|
| Tangents to a circle from a point outside the circle - use of the
tangency condition
|
| Example:
Find the angle between tangents drawn from the point
A(-1,
7) to the circle
x2
+ y2 = 25 . |
| Solution:
Equations of tangents we
find from the system formed by equation of the line and the
tangency condition, |
|
A(-1,
7) => (1)
y =
mx + c => c =
m + 7
=> (2) |
|
(2) r2·(m2
+ 1)
= c2 |
|
|
|
25(m2
+ 1)
= (m + 7)2 |
| 12m2
-
7m
-
12 = 0 => m1
= -
3/4
and
m2
= 4/3 |
| c1
= -
3/4 + 7 = 25/4 and
c2
= 4/3 + 7 = 25/3 |
| therefore,
the equations of tangents, |
| t1
::
y =
-
(3/4)x + 25/4 and
t2
::
y =
(4/3)x + 25/3. |
| Slopes of tangents satisfy perpendicularity condition, that is
|
| m1
= -
1/m2
=>
j =
90°. |
|
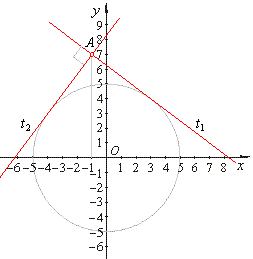 |
|
|
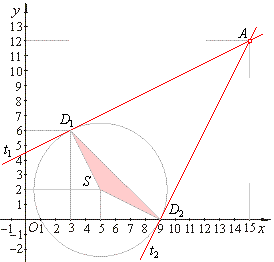
| Example:
Find the area of the triangle made by points of contact of tangents, drawn from the point |
| A(15,
12) to the circle
(x
-
5)2 + (y -
2)2 =
20 , and the center
S of the circle. |
Solution:
From the system of equations formed by equation of the line through point
A
and the condition of
tangency for the circle with the center at S(p,
q), we calculate slopes and intersections of tangents, thus |
| A(15,
12)
=> (1) y =
mx + c, c =
12 -
15m
=>
(2) |
|
(2) r2·(m2
+ 1) = (q -m
p -
c)2 |
|
|
|
S(5,
2)
and
r2
= 20
=>
(2) |
| 20·(m2
+ 1) = (2 -
5m
-
12 +
15m)2 |
| 2m2
-
5m
+ 2 = 0
=>
m1
= 1/2
and
m2
= 2, |
| as
c =
12 -
15m
then c1
= 9/2 and
c2
= -
18 |
| therefore,
the equations of tangents, |
| t1
::
y =
(1/2)x + 9/2
and
t2
::
y =
2x -
18. |
|
 |
|
| Coordinates of the tangency points we calculate
by solving system of equations formed by equations of tangents and equation of the
circle, thus |
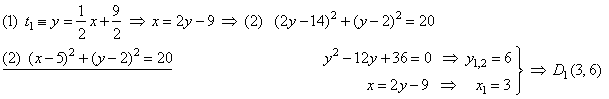 |
| and
the tangency point D2, |
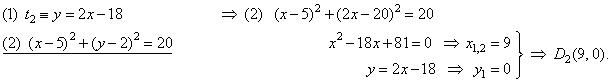 |
| The
area of the triangle SD1D2, |
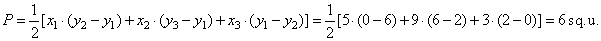 |
|
|
|
|
|
|
|